Transport Equation
The Transport Equation is given by:
$$\partial_t u(t,x)+\partial_x u(t,x)=0\:\:\:\rightarrow \:\:\:\langle \nabla u,v\rangle=0\:\:\: for\:\:\: v=(1,1)$$
We therefore have a look at:
$$
v_\zeta (t)=u(t,\zeta+t)\:\:\:\:\rightarrow \:\:\:\:\dfrac{d}{dt}v_\zeta (t)=\partial_t u(t,\zeta+t)+\partial_x u(t,\zeta+t)=0
$$
one now finds
$$
v_\zeta (t)=const.=f(\zeta)\:\:\:\:\rightarrow\:\:\:\: u(t,x)=f(x-t)\:\:\:\: since \:\:\:\:x=\zeta+t
$$
The Transport equation can also be solved numerically with Runge Kutta methods.
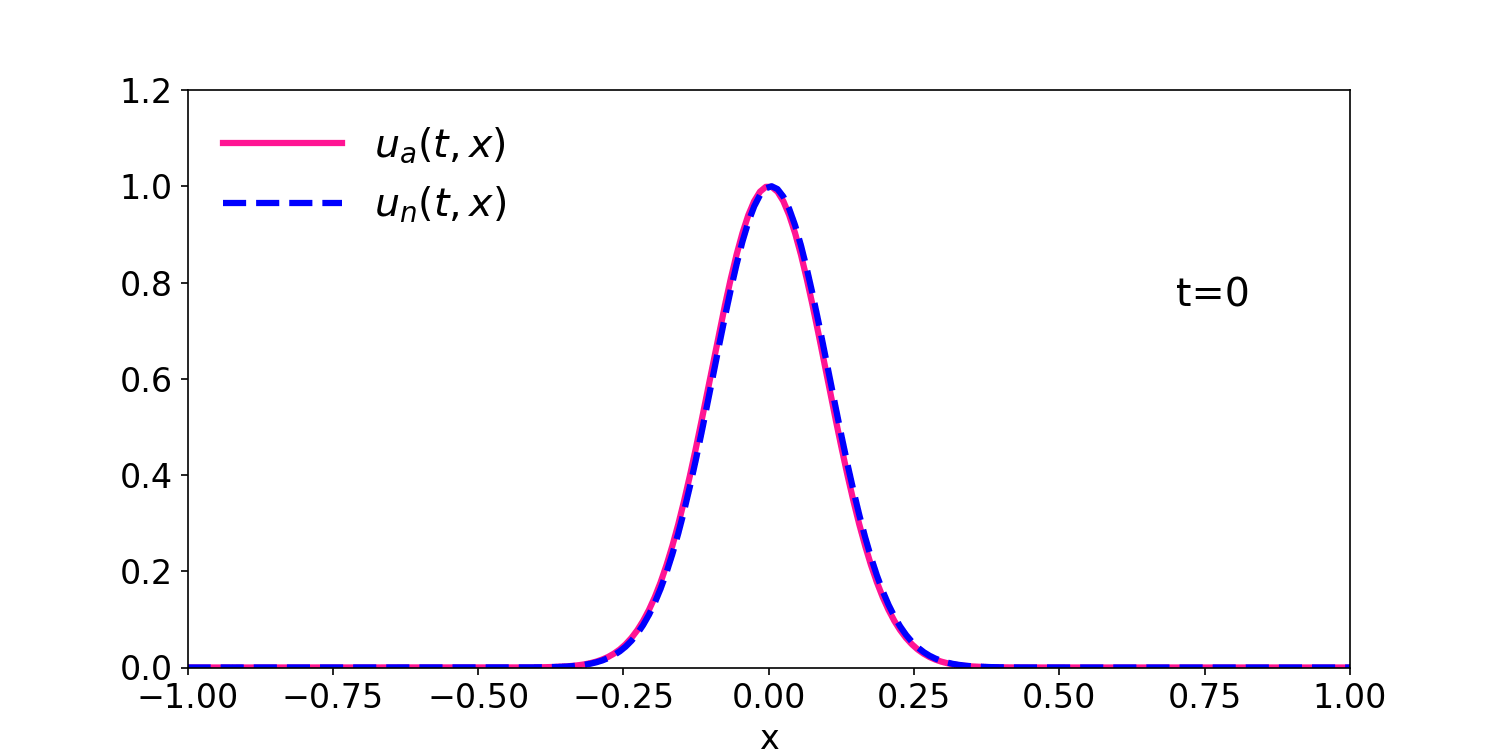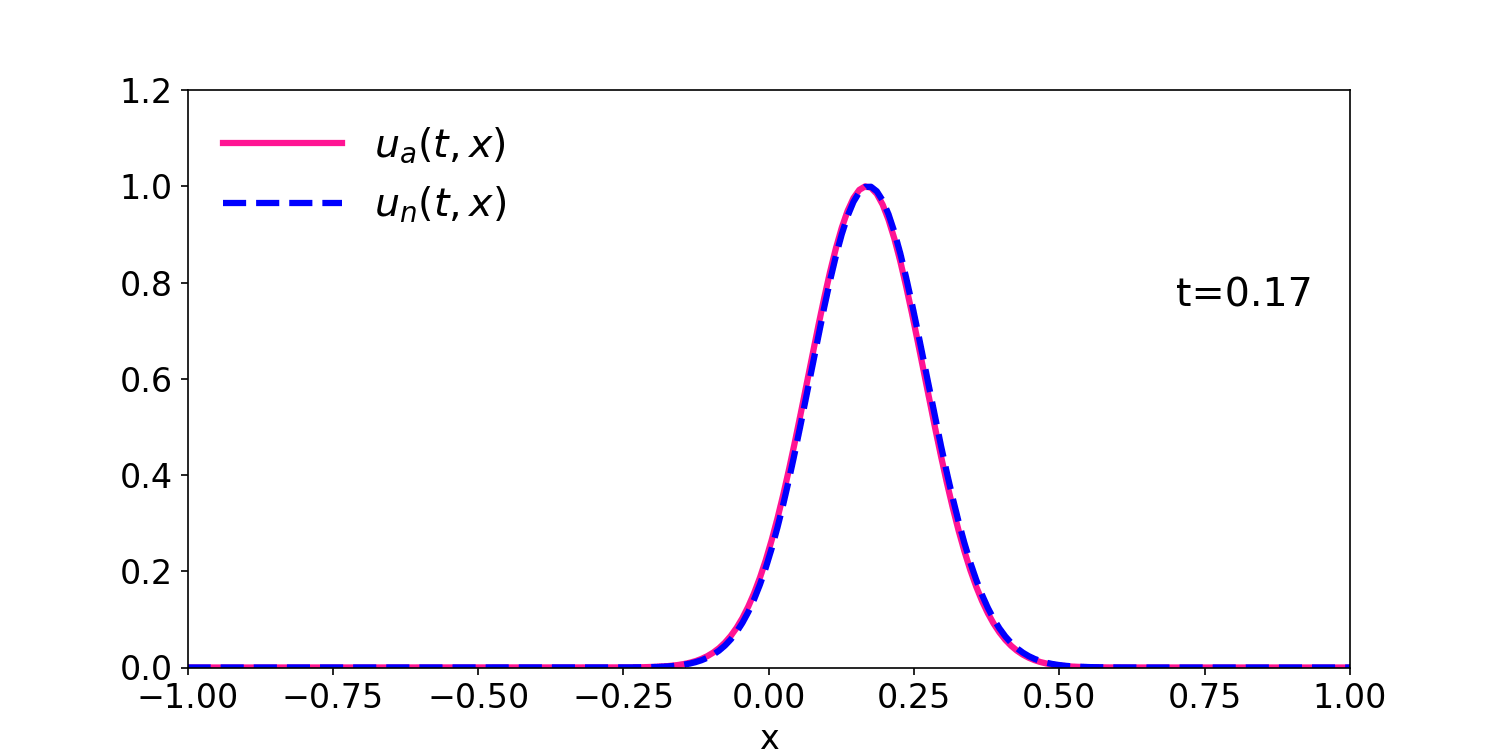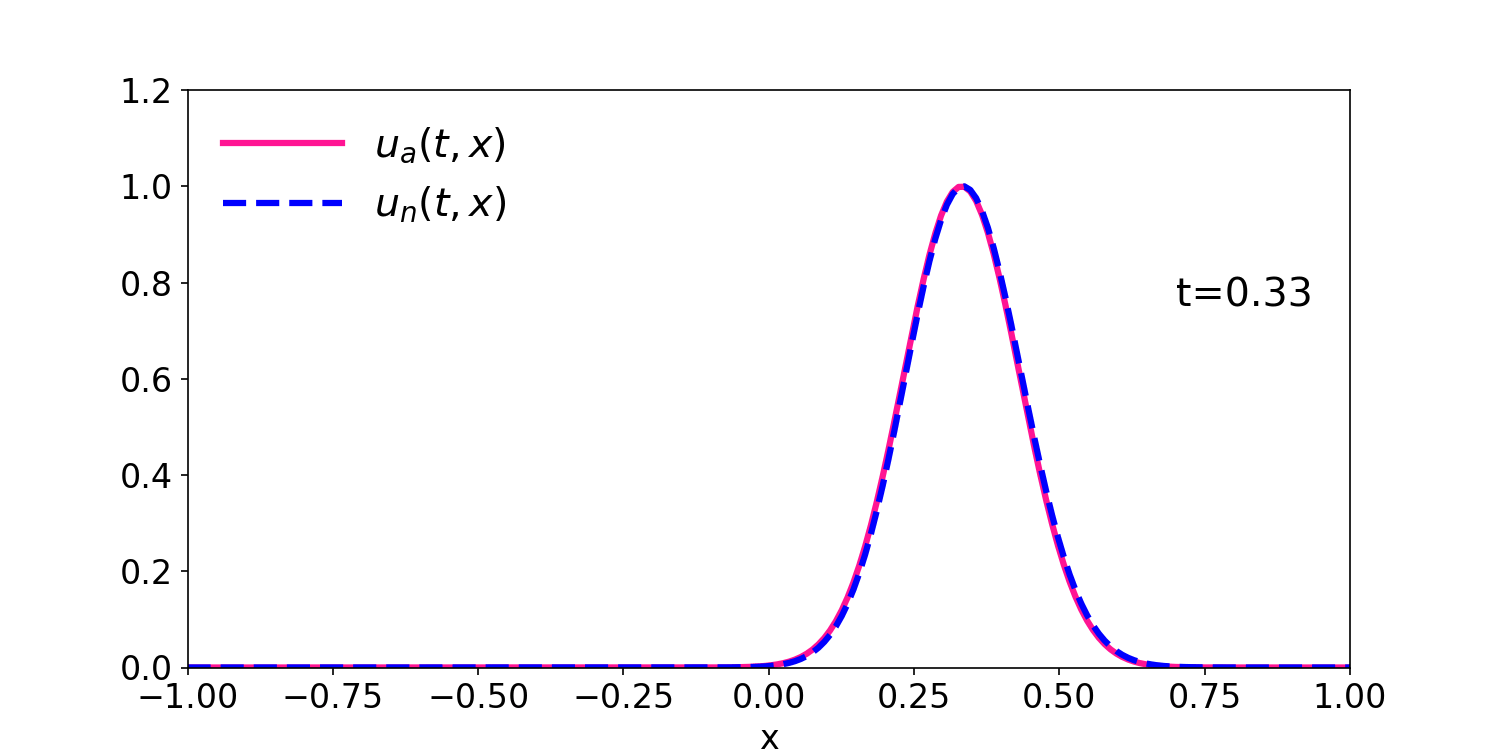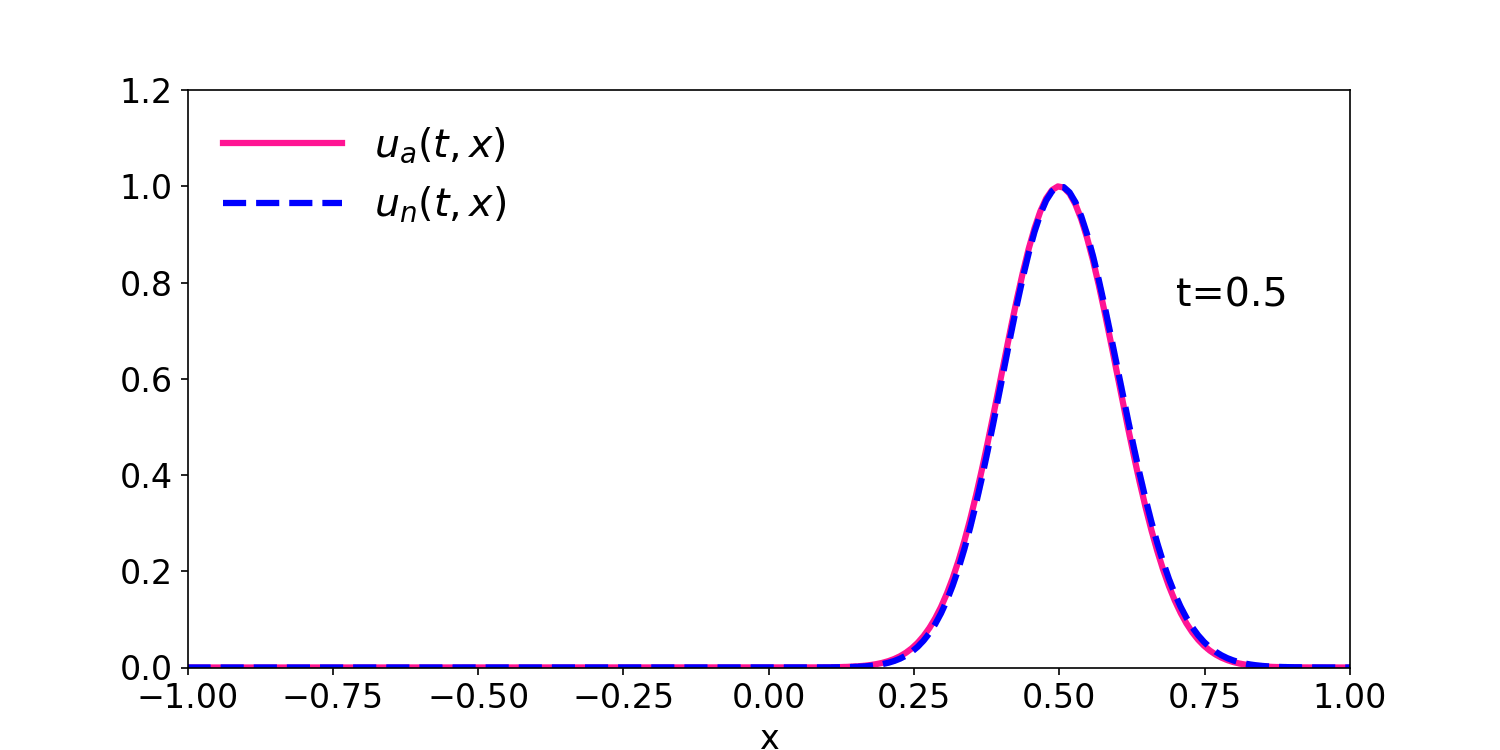
Figure 1: comparison of the numerical and analytical solution for \(u(0,x)=e^{-50\:x^2}\) and \(u(t,x)=e^{-50\:(x-t)^2}\).
"""The code below was written by @author: https://github.com/DianaNtz and is an
implementation of the Runge Kutta method for the transport equation"""
import numpy as np
import matplotlib.pyplot as plt
import os
import imageio
#some initial values
filenames = []
nx=200
x0=-1
xfinal=1
h=(xfinal-x0)/(nx-1)
x=np.linspace(x0,xfinal,nx)
nt=120*1
t0=0
tfinal=0.5
dt=(tfinal-t0)/(nt-1)
#finite difference derivative
def first(D):
n=len(D)
Dr=np.zeros(n)
Dr[0]=(D[0+1]-D[0])/(h)
Dr[n-1]=(D[n-1]-D[n-1-1])/(h)
for i in range(0,n-2):
Dr[i+1]=(D[i+2]-D[i])/(2*h)
return Dr
un=np.e**(-100*x**2/2)
t=t0
#Runge Kutta time integration loop
for j in range(0,nt):
ua=np.e**(-100*(x-t)**2/2)
k1=-dt*first(un)
k2=-dt*first(un+0.5*k1)
k3=-dt*first(un+0.5*k2)
k4=-dt*first(un+k3)
un=un+(k1+2*k2+2*k3+k4)/6
if(j%1==0):
ax1 = plt.subplots(1, sharex=True, figsize=(10,5))
plt.plot(x,ua,color='deeppink',linestyle='-',linewidth=3.0,label="$u_{a} (t,x)$")
plt.plot(x,un,color='blue',linestyle='--',linewidth=3.0,label="$u_{n} (t,x)$")
plt.xlabel("x",fontsize=16)
plt.ylim([0,1.2])
#plt.ylim([-1,1])
plt.xlim([-1,1])
#plt.xlim([0,2*np.pi])
plt.xticks(fontsize= 16)
plt.yticks(fontsize= 16)
plt.text(0.7, 0.75,"t=".__add__(str(round(t,2))),fontsize=19 )
plt.legend(loc=2,fontsize=19,handlelength=3,frameon=False)
filename ='bla{0:.0f}.png'.format(int(j/1))
filenames.append(filename)
plt.savefig(filename,dpi=150)
plt.close()
t=t+dt
#creating animation
with imageio.get_writer('transport.gif', mode='I') as writer:
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
for filename in set(filenames):
os.remove(filename)