Embedded Runge Kutta Methods
Initial value problems are specified as:
$$\dfrac{d}{dt}u(t)=f(t,u(t)),\:\:\:\:\:\:\:\:\:\:\:u(t_0)=u_0$$
These kind of problems can easely be solved by Runge Kutta methods:
$$u_{n+1}=u_n+dt\sum\limits_{j=1}^{s}b_jk_j,\:\:\:\:\:\:\mathrm{with}\:\:\:\:\:\: k_j=f(t_n+c_jdt,u_n+dt\sum\limits_{i=1}^{j-1}a_{ji}k_i)$$
The needed coefficients are often written in a Butcher-Tableau:
$$\begin{array}
{c|cccc}
c_1&0\\
c_2 & a_{21}\\
\vdots &\vdots & \ddots \\
c_s& a_{s1}& \ldots& a_{ss-1}&0\\
\hline
& b_1 &b_2 & \ldots&b_s
\end{array}$$
An embedded Runge Kutta consist of two separate methods of order \(p\) and \(p-1\) with almost same Butcher-Tableau except for the \(b_i\) coefficients.
An example is the Dormand Prince Method:
$$\begin{array}
{c|ccccccc}
0&0& & & & & & &\\
1/5 & 1/5& & & & & &\\
3/10&3/40 & 9/40 & & & & &\\
4/5& 44/45& -56/15& 32/9& & & &\\
8/9& 19372/6561& -25360/2187& 64448/6561&-212/729 & & &\\
1& 9017/3168& -355/33& 46732/5247&49/176 &-5103/18656 & &\\
1& 35/384&0 & 500/1113&125/192&-2187/6784&11/84&0\\
\hline
5th& 35/384 &0 & 500/1113&125/192&-2187/6784&11/84&0\\
4th&5179/57600&0&7571/16695&393/640&-92097/339200&187/2100&1/40
\end{array}$$
\(\:\)
A very helpful feature of embedded Runge Kutta methods is that the error can easily estimated by: $$err_n=dt_n\sum\limits_{j=1}^{s}(b_j-\tilde{b_j})k_j$$ With this estimate the step size for the next time step can be calculated to: $$dt_{n+1}=dt_n\bigg(\frac{tol}{\|err_n\|}\bigg)^{1/p}$$ Where \(tol\) is the a desired accuracy. A slightly different approach is: $$dt_{n+1}=dt_nS\bigg(\frac{tol}{\|err_n\|}\bigg)^{1/p}\:\:\mathrm{for}\:\:tol\geq err_n$$ and $$dt_{n+1}=dt_nS\bigg(\frac{tol}{\|err_n\|}\bigg)^{1/(p-1)}\:\:\mathrm{for}\:\:tol < err_n$$ Where \(S\) is the so called safety factor which is close to 1. Lets have a look at the following analytical test case: $$\dfrac{d}{dt}u(t)=-(t-a)u(t),\:\:\:\:\:\:\:\:\:\:\:u(0)=C$$ Its analytical solution is: $$u_a(t)=Ce^{-\frac{1}{2}(t-2a)t}$$
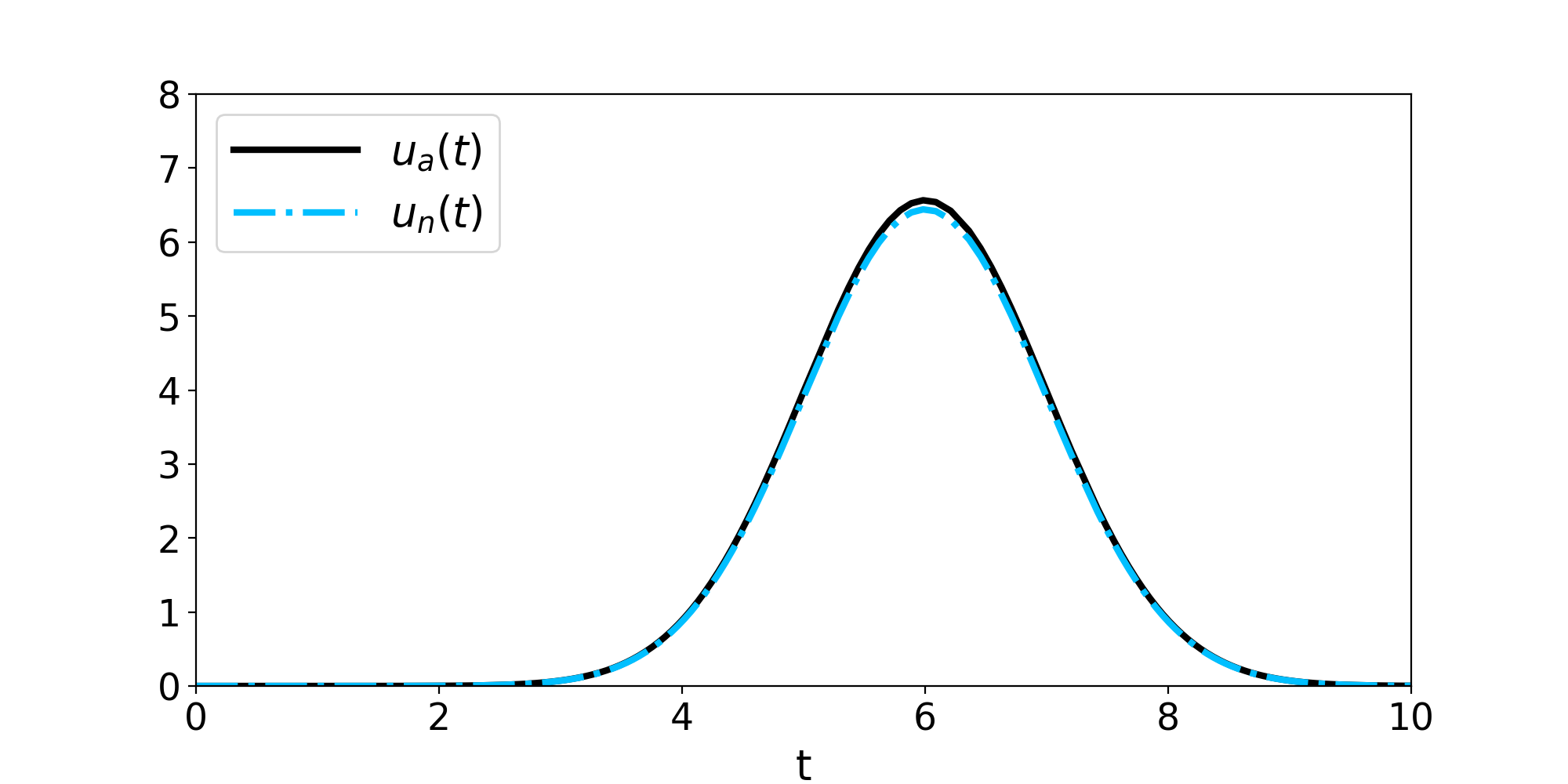
Figure 1: Comparison of the analytical solution \(u_a(t)\) and numerical solution \(u_n(t)\) obtained from the Dormand Prince method with step size control.
Notice however that one has set \(t_0=0\:\), \(t_{final}=10\:\), \(C=10^{-7}\:\) and
\(a=6\:\). The initial step size was set to \(dt=0.3125\) and the wanted accuracy to \(tol=10^{-8}\).
"""
The code below was written by https://github.com/DianaNtz and
is an implementation of the embedded Dormand-Prince Runge-Kutta Method with adaptive
step size control.
"""
import numpy as np
import matplotlib.pyplot as plt
#some initial values
t0=0
tfinal=10
steps=2**5
dt=(tfinal-t0)/(steps)
u0=0.0000001
a=6
#error tolerance
tol=10**(-8)
#differential equation function f
def f(t,u):
return -(t-a)*u
#setting up arrays
t=np.empty(1, dtype='double')
t[0]=t0
tn=t0
u=np.empty(1, dtype='double')
u[0]=u0
un=u0
#time integration loop
while(tn<=10):
k1=dt*f(tn,un)
k2=dt*f(tn+(1/5)*dt,un+(1/5)*k1)
k3=dt*f(tn+(3/10)*dt,un+(3/40)*k1+(9/40)*k2)
k4=dt*f(tn+(4/5)*dt,un+(44/45)*k1-(56/15)*k2+(32/9)*k3)
k5=dt*f(tn+(8/9)*dt,un+(19372/6561)*k1-(25360/2187)*k2+(64448/6561)*k3-(212/729)*k4)
k6=dt*f(tn+dt,un+(9017/3168)*k1-(355/33)*k2+(46732/5247)*k3+(49/176)*k4
-(5103/18656)*k5)
k7=dt*f(tn+dt,un+(35/384)*k1+(500/1113)*k3+(125/192)*k4-(2187/6784)*k5+(11/84)*k6)
#order 5 coefficients
b1=35/384
b2=0
b3=500/1113
b4=125/192
b5=-(2187/6784)
b6=11/84
b7=0
#order 4 coefficients
tildeb1=5179/57600
tildeb2=0
tildeb3=7571/16695
tildeb4=393/640
tildeb5=-(92097/339200)
tildeb6=187/2100
tildeb7=1/40
err=(b1-tildeb1)*k1+(b2-tildeb2)*k2+(b3-tildeb3)*k3+(b4-tildeb4)*k4+(b5-tildeb5)*k5
+(b6-tildeb6)*k6+(b7-tildeb7)*k7
print(err)
un=un+b1*k1+b2*k2+b3*k3+b4*k4+b5*k5+b6*k6+b7*k7
tn=tn+dt
t=np.append(t,tn)
u=np.append(u,un)
if(np.abs(err)>tol):
dt=0.95*dt*(tol/np.abs(err))**(0.25)
if(np.abs(err) <= tol):
dt=0.95*dt*(tol/np.abs(err))**(0.2)
#analytical solution
ua=u0*np.exp(-0.5*(t-a*2)*t)
#plotting analytical vs numerical solutions for order 5
ax1 = plt.subplots(1, sharex=True, figsize=(10,5))
plt.plot(t,ua,color='black',linestyle='-',linewidth=3,label="$u_a(t)$")
plt.plot(t,u,color='deepskyblue',linestyle='-.',linewidth=3,label = "$u_n(t)$")
plt.xlabel("t",fontsize=19)
plt.ylabel(r' ',fontsize=19,labelpad=20).set_rotation(0)
plt.ylim([0,8])
plt.xlim([t0,tfinal])
plt.xticks(fontsize= 17)
plt.yticks(fontsize= 17)
plt.legend(loc=2,fontsize=19,handlelength=3)
plt.savefig("stepsize.pdf")
plt.show()Dense Runge Kutta methods are using one extra function evaluation to interpolate values between two time steps: $$u(t_n+\sigma dt)=u(t_n)+dt\sum\limits_{j=1}^{s+1}b'_j(\sigma)k_j$$ For Dormand Prince one gets the more precise formula: $$u(t_n+\sigma dt)=u(t_n)+dt\sigma\sum\limits_{j=1}^{8}b'_jk_j$$ The additional coefficients for \(s+1\) can be calculated from: $$\begin{pmatrix} (c)_{3-7}&c_8&0&0\\ (c^2)_{3-7}&c_8^2&0&0\\ (c^3)_{3-7}&c_8^3&0&0\\ (c^4)_{3-7}&c_8^4&0&0\\ (Ac^3)_{3-7}&0&0&0\\ (A^2e_2)_{3-7}&0&-1&0\\ (Ae_2\cdot c)_{3-7}&0&0&-c_8\\ (Ae_2)_{3-7}&0&0&-1 \end{pmatrix}\begin{pmatrix} b'_3\\ b'_4\\ b'_5\\ b'_6\\ b'_7\\ b'_8\\ \gamma_1\\ \gamma_2 \end{pmatrix}= \begin{pmatrix} \frac{1}{2}\sigma\\ \frac{1}{3}\sigma^2\\ \frac{1}{4}\sigma^3\\ \frac{1}{5}\sigma^4\\ \frac{1}{20}\sigma^4-\gamma\\ 0\\ 0\\ 0 \end{pmatrix}$$ and $$\begin{pmatrix} c_2&c_3&c_4&c_5&1\\ c_2^2&c_3^2&c_4^2&c_5^2&1\\ c_2^3&c_3^3&c_4^3&c_5^3&1\\ 0&a_{32}&a_{42}&a_{52}&0\\ 1&0&0&0&0\\ \end{pmatrix}\begin{pmatrix} a_{82}\\ a_{83}\\ a_{84}\\ a_{85}\\ a_{87}\\ \end{pmatrix}= \begin{pmatrix} \frac{1}{2}c_8^2-a_{86}\\ \frac{1}{3}c_8^3-a_{86}\\ \frac{\gamma}{b'_8}-a_{86}\\ -\frac{\gamma_1}{b'_8}-a_{62}a_{86}\\ -\frac{\gamma_2}{b'_8}\\ \end{pmatrix}$$ With: $$b'_1=1-\sum\limits_{j=3}^8,\:\:\:\:\:\:\:\:\:\:b'_2=0,\:\:\:\:\:\:\:\:\:\:a_{81}=c_8-\sum\limits_{j=2}^7a_{8j}$$ Note that \(c_8\), \(\gamma\) and \(a_{86}\) can be chosen almost freely with only some minor restrictions on \(c_8\). Further note that: $$e_2=\begin{pmatrix}0&1&0&0&0&0&0\end{pmatrix}^T,\:\:\:\:\:c=\begin{pmatrix}c_1&c_2&c_3&c_4&c_5&c_6&c_7\end{pmatrix}^T,\:\:\:\:\: A=\begin{pmatrix}0&0&0&...\\ a_{21}&0&0&...\\ a_{31}&a_{32}&0&...\\ ...&...&...&.. \end{pmatrix}$$ Lets have again a look at our analytical test case: $$\dfrac{d}{dt}u(t)=-(t-a)u(t)\:\xrightarrow{}\:u_a(t)=u_0e^{-\frac{1}{2}(t-2a)t}$$ To test the convergence of the above example one can use: $$error(N)=\|u_a(t)-u_N(t)\|_{sup},\:\:\:\:\:\:\:\:C(N)=\dfrac{error(N)}{error(2N)}\xrightarrow{}2^p$$ Where \(N\) is the number of time steps and therefore related to \(dt\).
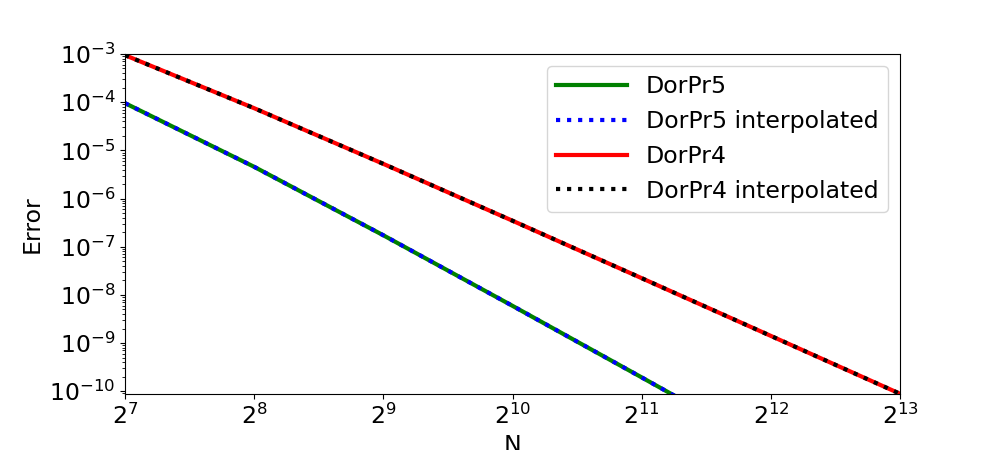
Figure 2: Comparison of the convergence for the interpolated dense Runge Kutta methods and the non interpolated standard embedded Runge Kutta method. Notice that one has set \(t_0=0\:\), \(t_{final}=10\:\), \(C=10^{-7}\:\) and \(a=6\:\).
"""
The code below was written by https://github.com/DianaNtz and
is an implementation of dense Runge-Kutta methods for the Dormand–Prince
embedded Runge-Kutta method of order 4 and 5.
"""
import numpy as np
import matplotlib.pyplot as plt
#differential equation function f
def f(t,u):
return -(t-6)*u
#Dormand–Prince embedded Runge-Kutta method of order 4 and 5
def RungeKutta(t0,tfinal,steps,u0,string):
dt=(tfinal-t0)/(steps)
t=np.zeros(steps+1, dtype='double')
tn=t0
u=np.zeros(steps+1, dtype='double')
un=u0
n=0
if(string=="DorPr5" or string=="DorPr4"):
n=7
tcoff=np.array([0,1/5,3/10,4/5,8/9,1,1])
c=np.array([[0,0,0,0,0,0],[1/5,0,0,0,0,0],[3/40,9/40,0,0,0,0],[44/45,-56/15,32/9,0,0,0],
[19372/6561,-(25360/2187),(64448/6561),-(212/729),0,0],
[(9017/3168),-(355/33),(46732/5247),(49/176),-(5103/18656),0],
[(35/384),0,(500/1113),(125/192),-(2187/6784),(11/84)]])
if(string=="DorPr5"):
b=np.array([35/384,0,500/1113,125/192,-(2187/6784),11/84,0])
if(string=="DorPr4"):
b=np.array([5179/57600,0,7571/16695,393/640,-(92097/339200),187/2100,1/40])
k=np.zeros([n, steps+1])
for i in range(0,steps+1):
t[i]=tn
u[i]=un
for j in range(0,n):
if(j==0):
k[j][i]=dt*f(tn+tcoff[0]*dt,un)
else:
bb=c[j][0:j]
bbb=0
for l in range(0,len(bb)):
bbb=bbb+bb[l]*k[l][i]
k[j][i]=dt*f(tn+tcoff[j]*dt,un+bbb)
bbb=0
for g in range(0,n):
bbb=bbb+b[g]*k[g][i]
un=un+bbb
tn=tn+dt
return t,u,k,string
#dense Runge-Kutta method
def interpolate(t,u,k,sigma,string,c8=2/5,gamma=-1/30000,a86=1/20):
dt=t[1]-t[0]
tneu=t+sigma*dt
if(string=="DorPr5" or string=="DorPr4"):
sig=np.array([1/2*sigma, 1/3*sigma**2,1/4*sigma**3,1/5*sigma**4, 1/20*sigma**4-gamma,0,0,0])
A=np.array([[ 3/10, 4/5, 8/9, 1, 1, c8, 0, 0],
[ (3/10)**2, (4/5)**2, (8/9)**2, 1, 1, c8**2, 0, 0],
[ (3/10)**3, (4/5)**3, (8/9)**3, 1, 1, c8**3, 0, 0],
[ (3/10)**4, (4/5)**4, (8/9)**4, 1, 1, c8**4, 0, 0],
[(1/5)**3*(9/40), -(1/5)**3*(56/15)+(3/10)**3*(32/9), -(1/5)**3*(25360/2187)
+(3/10)**3*(64448/6561)-(4/5)**3*(212/729), -(1/5)**3*(355/33)
+(3/10)**3*(46732/5247)+(4/5)**3*(49/176)-(8/9)**3*(5103/18656),
(3/10)**3*(500/1113)+(4/5)**3*(125/192)-(8/9)**3*(2187/6784)+11/84, 0, 0, 0],
[0, 32/9*(9/40), (64448/6561)*(9/40)+(212/729)*(56/15), (46732/5247)*(9/40)
-(49/176)*(56/15)+(5103/18656)*(25360/2187), (500/1113)*(9/40)
-(125/192)*(56/15)+(2187/6784)*(25360/2187)-(11/84)*(355/33), 0, -1, 0],
[9/40*(3/10), -56/15*(4/5), -25360/2187*(8/9),-355/33, 0, 0, 0, -c8],
[9/40, -56/15, -25360/2187,-355/33, 0, 0, 0, -1]
])
Ainv=np.linalg.inv(A)
vb8=Ainv.dot(sig)
bstrich8=vb8[-3]
gamma1=vb8[-2]
gamma2=vb8[-1]
vec=np.array([0.5*c8**2-a86,(1/3)*c8**3-a86,gamma/bstrich8-a86,-gamma1/bstrich8-a86*(-355/33),
-gamma2/bstrich8])
C=np.array([[1/5,3/10, 4/5, 8/9, 1],
[(1/5)**2,(3/10)**2, (4/5)**2, (8/9)**2, 1],
[(1/5)**3,(3/10)**3, (4/5)**3, (8/9)**3, 1],
[0,9/40, -56/15, -25360/2187, 0],
[1, 0, 0, 0, 0]
])
Cinv=np.linalg.inv(C)
va8=Cinv.dot(vec)
b1strich=1-vb8[0]-vb8[1]-vb8[2]-vb8[3]-vb8[4]-vb8[5]
a81=c8-np.sum(va8)-a86
avec8=np.array([a81,va8[0],va8[1],va8[2],va8[3],a86,va8[4]])
bstrichvec=np.array([b1strich,0,vb8[0],vb8[1],vb8[2],vb8[3],vb8[4],vb8[5]])
k8=dt*f(t+c8*dt,u+avec8[0]*k[0]+avec8[1]*k[1]+avec8[2]*k[2]+avec8[3]*k[3]+avec8[4]*k[4]
+avec8[5]*k[5]+avec8[6]*k[6])
uneu=u+(bstrichvec[0]*k[0]+bstrichvec[1]*k[1]+bstrichvec[2]*k[2]+bstrichvec[3]*k[3]
+bstrichvec[4]*k[4]+bstrichvec[5]*k[5]+bstrichvec[6]*k[6]+bstrichvec[7]*k8)*sigma
return tneu,uneu
#plotting and error calculation
nende=13
nstart=7
n=np.zeros(nende-nstart+1, dtype='double')
error=np.zeros(nende-nstart+1, dtype='double')
errorinter=np.zeros(nende-nstart+1, dtype='double')
method=["DorPr4","DorPr5"]
string=""
for j in range(0,len(method)):
#print(method[j])
string=string+method[j]+":"+"\n"
for i in range(nstart,nende+1):
t0=0
tfinal=10
steps=2**i
u0=0.0000001
t,u,k,s= RungeKutta(t0,tfinal,steps,u0,method[j])
ua=u0*np.exp(-0.5*(t-6*2)*t)
ax1 = plt.subplots(1, sharex=True, figsize=(10,5))
plt.plot(t,ua,color='black',linestyle='-',linewidth=3,label="$u_a(t)$")
plt.plot(t,u,color='deepskyblue',linestyle='-.',linewidth=3,label = "$u_n(t)$")
plt.xlabel("t",fontsize=19)
plt.ylabel(r' ',fontsize=19,labelpad=20).set_rotation(0)
plt.ylim([0,np.max(u)])
plt.xlim([t0,tfinal])
plt.xticks(fontsize= 17)
plt.yticks(fontsize= 17)
plt.title(s+" n={0:.0f}".format(2**i),fontsize=22)
plt.legend(loc=2,fontsize=19,handlelength=3)
plt.show()
dt=(tfinal-t0)/(steps)
err=np.max(np.abs(ua[:steps]-u[:steps]))
string=string+" n=2^"+str(i)+" Error: "+str(err)+"\n"
error[i-nstart]=err
t1,u1=interpolate(t,u,k,0.2,s)
ua1=u0*np.exp(-0.5*(t1-6*2)*t1)
ax1 = plt.subplots(1, sharex=True, figsize=(10,5))
plt.plot(t1,ua1,color='black',linestyle='-',linewidth=3,label="$u_a(t)$")
plt.plot(t1,u1,color='deepskyblue',linestyle='-.',linewidth=3,label = "$u_{inter}(t)$")
plt.xlabel("t",fontsize=19)
plt.ylabel(r' ',fontsize=19,labelpad=20).set_rotation(0)
plt.ylim([0,np.max(u1)])
plt.xlim([t1[0],t1[-1]])
plt.xticks(fontsize= 17)
plt.yticks(fontsize= 17)
plt.title(s+" interpolated n={0:.0f}".format(2**i),fontsize=22)
plt.legend(loc=2,fontsize=19,handlelength=3)
plt.show()
errinter=np.max(np.abs(ua1[:steps]-u1[:steps]))
errorinter[i-nstart]=errinter
string=string+" n=2^"+str(i)+" Error: "+str(errinter)+" (interpolated)"+"\n"
n[i-nstart]=2**i
filename='data/method_'+s+'_error.npz'
np.savez(filename, n_loaded=n, error_loaded=error)
filename='data/method_'+s+'_errorinter.npz'
np.savez(filename, n_loaded=n, errorinter_loaded=errorinter)
if(j!=len(method)-1):
string=string+"\n"
print(string)
file = open("Errors.txt", "w")
file.write(string)
file.close()
#convergence order calculation
string=""
for j in range(0,len(method)):
s=method[j]
filename='data/method_'+s+'_error.npz'
error_data=np.load(filename)
error=error_data["error_loaded"]
n=error_data["n_loaded"]
filename='data/method_'+s+'_errorinter.npz'
errorinter_data=np.load(filename)
error_inter=errorinter_data["errorinter_loaded"]
for i in range(0,len(n)-1):
string=string+str(i)+"\n"
c1=error[i]/error[i+1]
c2=error_inter[i]/error_inter[i+1]
string=string+"2^p"+" for "+s+": "+str(c1)+"\n"+"2^p for "+s+": "+str(c2)+"(interpolated)"+"\n"
if(j!=len(method)-1):
string=string+"\n"
print(string)
file = open("Convergence.txt", "w")
file.write(string)
file.close()
filename='data/method_DorPr5_error.npz'
error_data=np.load(filename)
error5=error_data["error_loaded"]
n=error_data["n_loaded"]
filename='data/method_DorPr5_errorinter.npz'
errorinter_data=np.load(filename)
errorinter5=errorinter_data["errorinter_loaded"]
filename='data/method_DorPr4_error.npz'
error_data=np.load(filename)
error4=error_data["error_loaded"]
n=error_data["n_loaded"]
filename='data/method_DorPr4_errorinter.npz'
errorinter_data=np.load(filename)
errorinter4=errorinter_data["errorinter_loaded"]
ax1 = plt.subplots(1, sharex=True, figsize=(10,4.5))
plt.xscale('log', base=2)
plt.yscale('log', base=10)
plt.plot(n,error5,color='green',linestyle='-',linewidth=3,label = "DorPr5")
plt.plot(n,errorinter5,color='blue',linestyle=':',linewidth=3,label = "DorPr5 interpolated")
plt.plot(n,error4,color='red',linestyle='-',linewidth=3,label = "DorPr4")
plt.plot(n,errorinter4,color='k',linestyle=':',linewidth=3,label = "DorPr4 interpolated")
plt.xlabel("N",fontsize=17)
plt.ylabel('Error',fontsize=17)
plt.ylim([np.min(error4),10**(-3)])
plt.xlim([n[0],n[-1]])
plt.xticks(n,fontsize= 17)
plt.yticks(fontsize= 17)
plt.legend(loc=1,fontsize=17,handlelength=3)
#plt.title("Error Comparison",fontsize=22)
plt.savefig("figures/error.pdf")
plt.show()