Barycentric Interpolation
The Barycentric formula is given by:
$$p(z)=\dfrac{\sum_{j=0}^{n}\dfrac{\omega_j}{z-z_j}f_j}{\sum_{j=0}^{n}\dfrac{\omega_j}{z-z_j}},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\omega_j:=\dfrac{1}{\prod_{k\neq j}(z_j-z_k)}$$
Following figure shows the results for a Barycentric interpolated function f.
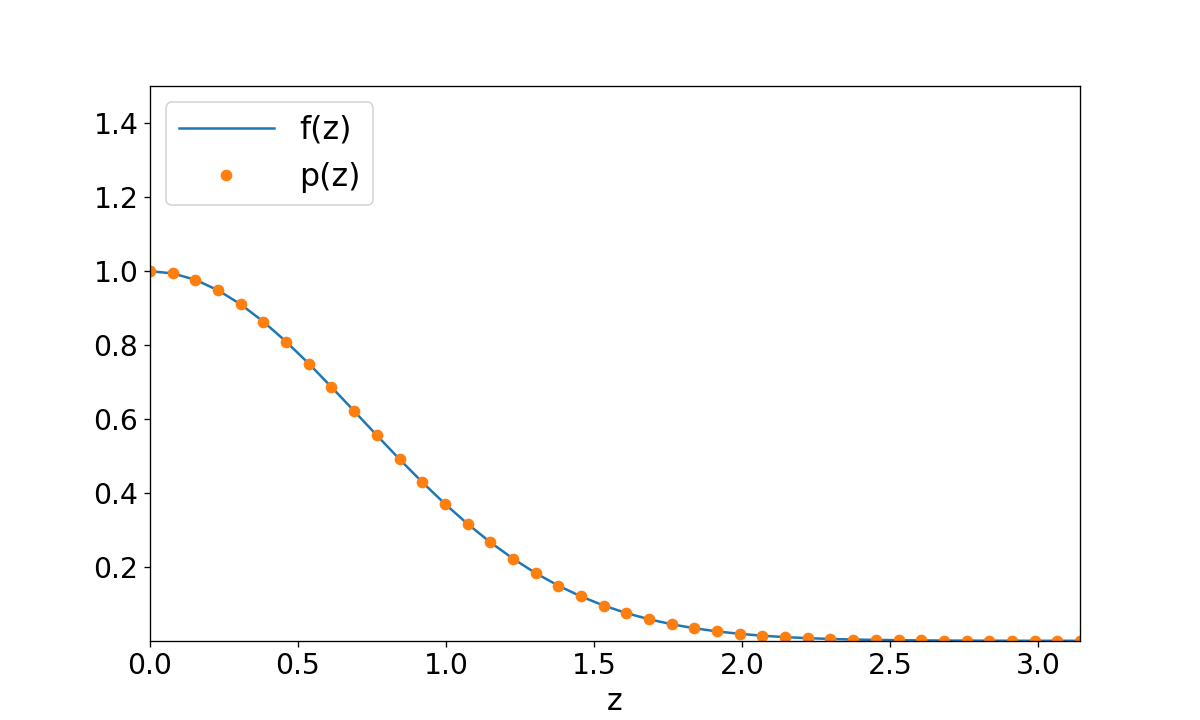
Figure 1: comparison of the interpolated \(p(z)\) and analytical values \(f(z)\) for \(f(z)=e^{-z^2}\).
"""The code below was written by @author: https://github.com/DianaNtz and is an
implementation of Barycentric Lagrange Interpolation in 1D and 2D."""
import numpy as np
import matplotlib.pyplot as plt
#create grid
zmin=0
zmax=np.pi
N=21
def grid(xmin,xmax,Nx):
x=np.zeros(Nx)
cx=(xmax-xmin)/2
dx=(xmax+xmin)/2
for j in range(0,Nx):
x[j]=-np.cos(j*np.pi/(Nx-1))*cx+dx
return x
#create test function 1D
def f(z):
return np.exp(-z**2)
zz=grid(zmin,zmax,N)
fzz=f(zz)
#1D Interpolation
def omega(zz):
N=len(zz)
w=np.zeros(N)
for i in range(0,N):
zi=zz[i]
wi=1
for j in range(0,i):
wi*=zi-zz[j]
for j in range(i+1,N):
wi*=zi-zz[j]
w[i]=1/wi
return w
w=omega(zz)
def p(z,fzz):
result=np.zeros(len(z))
for i in range (0,len(z)):
C1=0
C2=0
for j in range (0,len(w)):
if(np.abs(z[i]-zz[j])<0.00001):
C1=1
C2=fzz[j]
break
else:
C1=C1+w[j]/(z[i]-zz[j])
C2=C2+w[j]/(z[i]-zz[j])*fzz[j]
result[i]=C2/C1
return result
#interpolate test function into new grid
z=np.linspace(zmin,zmax,2*N)
ax1 = plt.subplots(1, sharex=True, figsize=(10,6))
plt.plot(z,f(z),"-",label="f(z)")
plt.plot(z,p(z,fzz),"o",label="p(z)")
plt.xlabel("z",fontsize=18)
plt.yticks(fontsize= 17)
plt.xticks(fontsize= 17)
plt.xlim(zmin,zmax)
plt.ylim(np.min(f(z)),np.max(f(z))+0.5)
plt.legend(loc=2,fontsize=19,handlelength=3)
plt.savefig("interpolation.png",dpi=120)
plt.show()
#2D Interpolation
def L(x0,x):
Lx=np.zeros(len(x))
ka=np.where(np.abs(x-x0)<=0.000001)
if(ka[0].size>0):
Lx[ka]=1
return Lx
wx=omega(x)
C1x=np.sum(wx/(x0-x))
C2x=wx/(x0-x)
Lx=C2x/C1x
return Lx
def interpolation2D(x0,y0,x,y,f):
Lx=L(x0,x)
Ly=L(y0,y)
C=0
L0=np.kron(Lx,Ly)
C=np.dot(L0,f)
return C
#create grid
Nx=60
Ny=30
xmin=0
xmax=1
ymin=0
ymax=np.pi
x=grid(xmin,xmax,Nx)
y=grid(ymin,ymax,Ny)
#create 2D test function
def fx(x):
return np.exp(-x**2)
def fy(y):
return np.exp(-(y-0.5)**2)
fxx=fx(x)
fyy=fy(y)
f=np.kron(fxx,fyy) #f[i+j*Ny] j x, i y
x0,y0=0.5,0.6
#compare interpolated with analytical result
print(interpolation2D(x0,y0,x,y,f))
print(fx(x0)*fy(y0))
References
[1] https://people.maths.ox.ac.uk/trefethen/barycentric.pdf
[1] https://people.maths.ox.ac.uk/trefethen/barycentric.pdf