Heat Equation

The heat equation is given by: $$\partial_tu-\Delta u=0\:\:\:\in\Omega \times (0,\infty),\:\:\:\: u(z,0)=f(z)\:\:\:\forall\: z\in\Omega\:\:\: and \:\:\:u(z,t)=0 \:\:\:\forall\: z\in\partial\Omega$$ With the Separation of variables ansatz $u(z,t)=F(z)G(t)$ one finds: $$\dfrac{\partial_t G}{G}=\dfrac{\Delta F}{F}=\lambda=const.\rightarrow \Delta f_j=\lambda_j f_j\:\:\: f_j=0\:\forall\: z\in\partial\Omega\rightarrow f=\sum c_jf_j$$ where $c_j:=\langle f,f_j \rangle$ the solution of the heat equation now becomes: $$u(z,t)=\sum c_j f_j(z) e^{\lambda_j t}$$

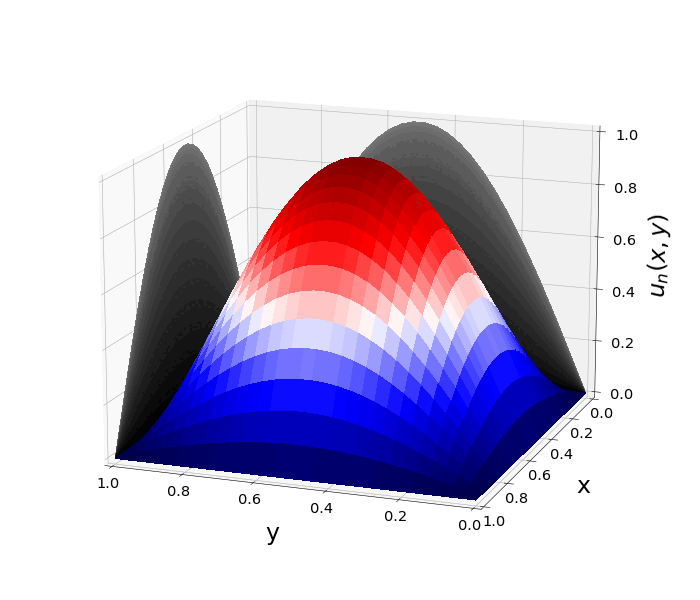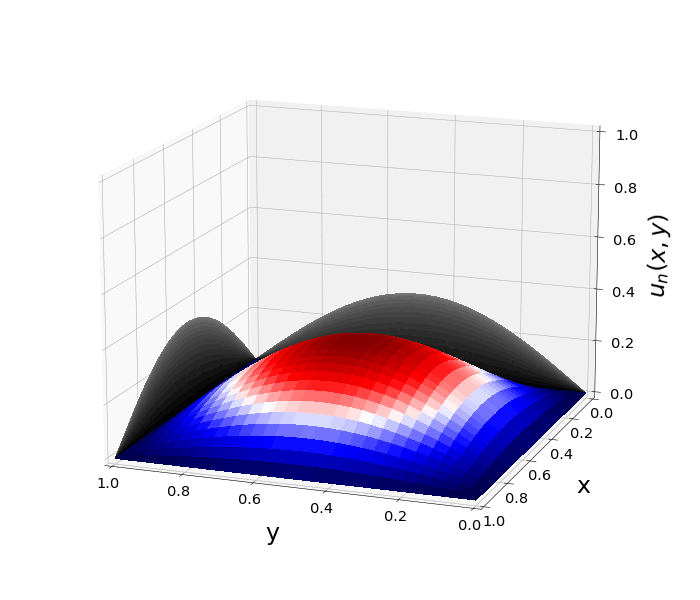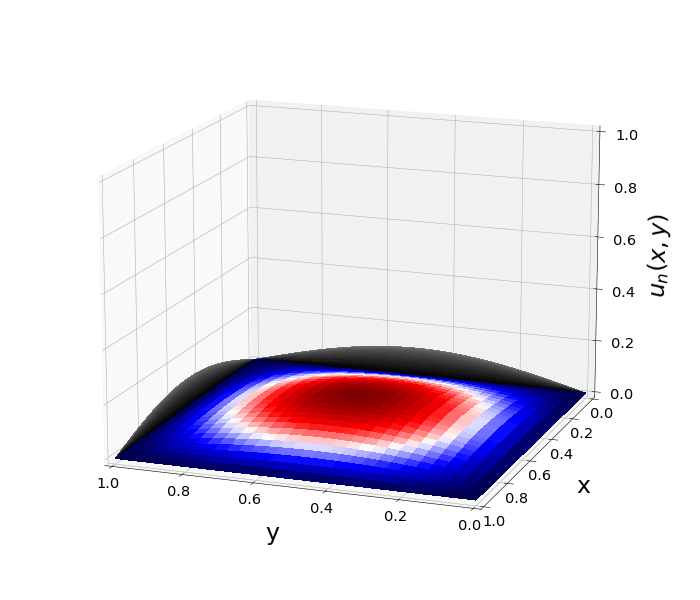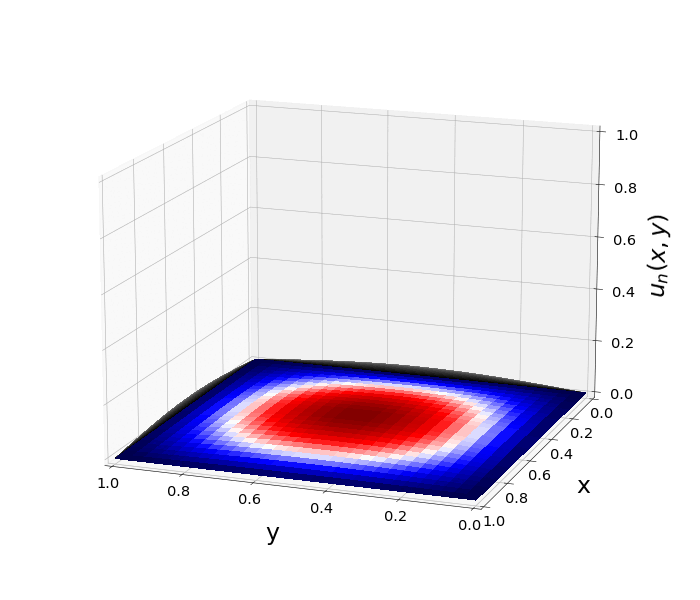
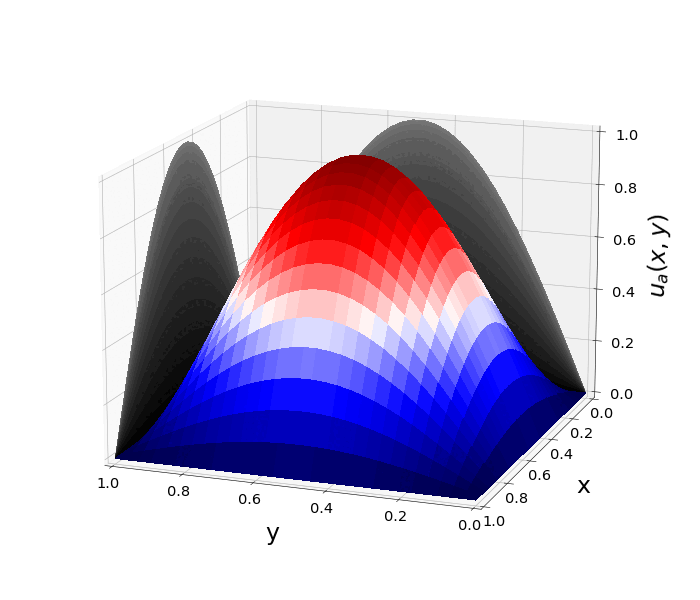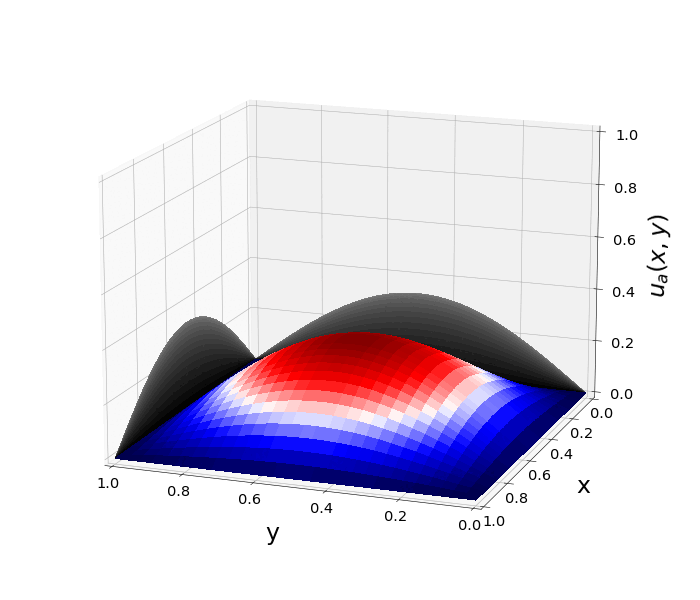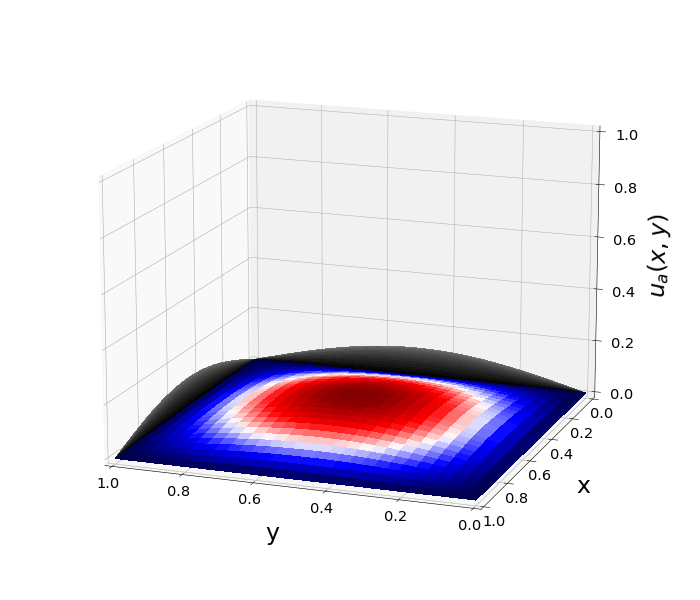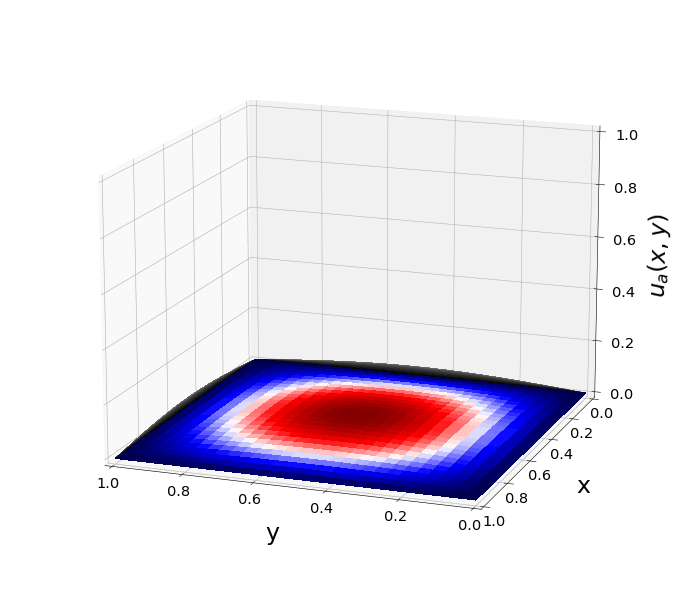
Figure 1: $\Omega=[0,1]\times[0,1]$ and $f(z)=f_j(z)=\sin{(\pi x)}\sin{(\pi y)}$ $\rightarrow$ $\lambda_j=-2\pi^2$ $u(x,y,t)=\sin{(\pi x)}\sin{(\pi y)}e^{-2\pi^2 t}$

References
[1] https://www.analysis.uni-hannover.de/fileadmin/analysis/Schrohe/Schrohe_Lehre/Partielle_Differentialgleichungen/pde6.pdf

To get the code go to my GitHub repository Heat

View Code

"""The code below was written by @author: https://github.com/DianaNtz and is an
implementation of the Runge Kutta method for the 2D heat equation"""

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import os
import imageio.v2 as imageio
nfilenames = []
afilenames = []
#some initial values
nx=30
x0=0
xfinal=1
dx=(xfinal-x0)/(nx-1)
x=np.linspace(x0,xfinal,nx)

ny=30
y0=0
yfinal=1
dy=(yfinal-y0)/(ny-1)
y=np.linspace(y0,yfinal,ny)

nt=450
t0=0
tfinal=0.17
dt=(tfinal-t0)/(nt-1)
t=0
#finite difference derivatives
def d2x(D):
    Dxx=np.zeros((ny,nx), dtype='double')
    for j in range(0,ny):
        for i in range(0,nx):
                 if(i==0):
                     Dxx[j][0]=(D[j][2]-2*D[j][1]+D[j][0])/(dx**2)
                 if(i==nx-1):
                     Dxx[j][nx-1]=(D[j][nx-1]-2*D[j][nx-1-1]+D[j][nx-1-2])/(dx**2)
                 if(i!=0 and i!=nx-1):
                     Dxx[j][i]=(D[j][i+1]-2*D[j][i]+D[j][i-1])/(dx**2)
    return Dxx

def d2y(D):
    Dyy=np.zeros((ny,nx), dtype='double')
    for j in range(0,ny):
        for i in range(0,nx):
                 if(j==0):
                     Dyy[j][0]=(D[2][i]-2*D[1][i]+D[0][i])/(dy**2)
                 if(j==ny-1):
                     Dyy[ny-1][i]=(D[ny-1][i]-2*D[ny-1-1][i]+D[ny-1-2][i])/(dy**2)
                 if(j!=0 and j!=ny-1):
                     Dyy[j][i]=(D[j+1][i]-2*D[j][i]+D[j-1][i])/(dy**2)
    return Dyy



un=np.empty([ny,nx], dtype='double')
ua0=np.empty([ny,nx], dtype='double')
for j in range(0,ny):
        for i in range(0,nx):
            un[j][i]=np.sin(np.pi*x[i])*np.sin(np.pi*y[j])
            ua0[j][i]=np.sin(np.pi*x[i])*np.sin(np.pi*y[j])

Y,X= np.meshgrid(y, x)

#Runge Kutta time integration loop
for k in range(0,nt):
    ua=ua0*np.e**(-2*np.pi**2*t)


    k1=dt*(d2x(un)+d2y(un))
    k2=dt*(d2x(un+0.5*k1)+d2y(un+0.5*k1))
    k3=dt*(d2x(un+0.5*k2)+d2y(un+0.5*k2))
    k4=dt*(d2x(un+k3)+d2y(un+k3))

    un=un+(k1+2*k2+2*k3+k4)/6
    for j in range(0,ny):
        un[j][0]=0
        un[j][nx-1]=0
    for i in range(0,nx):
        un[0][i]=0
        un[ny-1][i]=0
    err=np.abs(ua-un)
    if(k%5==0):

        fig = plt.figure(figsize=(14,12))
        axx = plt.axes(projection='3d')
        axx.plot_surface(Y, X, un.T,cmap=cm.seismic,antialiased=False)
        axx.contourf(Y, X, un.T,100, zdir='y', offset=x0,cmap=cm.binary)
        axx.contourf(Y, X, un.T,100, zdir='x',offset=yfinal,cmap=cm.binary)
        axx.view_init(azim=110,elev=15)
        axx.set_xlabel('y', labelpad=30,fontsize=34)
        axx.set_ylabel('x',labelpad=30,fontsize=34)
        axx.set_ylim(x0,xfinal)
        axx.set_xlim(y0,yfinal)
        axx.set_zlabel('$u_n(x,y)$',labelpad=40,fontsize=34)
        axx.set_zlim(0, 1)
        axx.zaxis.set_tick_params(labelsize=21,pad=18)
        axx.yaxis.set_tick_params(labelsize=21)
        axx.xaxis.set_tick_params(labelsize=21)
        plt.title("t=".__add__(str(round(t,2))),fontsize=34 )
        fig.subplots_adjust(left=0, right=1, bottom=0, top=1)
        nfilename ='nbla{0:.0f}.png'.format(int(k/5))
        nfilenames.append(nfilename)
        plt.savefig(nfilename,dpi=50)
        plt.close()

        fig = plt.figure(figsize=(14,12))
        axx = plt.axes(projection='3d')
        axx.plot_surface(Y, X, ua.T,cmap=cm.seismic,antialiased=False)
        axx.contourf(Y, X, ua.T,100, zdir='y', offset=x0,cmap=cm.binary)
        axx.contourf(Y, X, ua.T,100, zdir='x',offset=yfinal,cmap=cm.binary)
        axx.view_init(azim=110,elev=15)
        axx.set_xlabel('y', labelpad=30,fontsize=34)
        axx.set_ylabel('x',labelpad=30,fontsize=34)
        axx.set_ylim(x0,xfinal)
        axx.set_xlim(y0,yfinal)
        axx.set_zlabel('$u_a(x,y)$',labelpad=40,fontsize=34)
        axx.set_zlim(0, 1)
        axx.zaxis.set_tick_params(labelsize=21,pad=18)
        axx.yaxis.set_tick_params(labelsize=21)
        axx.xaxis.set_tick_params(labelsize=21)
        plt.title("t=".__add__(str(round(t,2))),fontsize=34 )
        fig.subplots_adjust(left=0, right=1, bottom=0, top=1)
        afilename ='abla{0:.0f}.png'.format(int(k/5))
        afilenames.append(afilename)
        plt.savefig(afilename,dpi=50)
        plt.close()

        print(np.max(err))

    t=t+dt
#creating animations
with imageio.get_writer('2Dheatnumerical.gif', mode='I') as writer:
    for filename in nfilenames:
        image = imageio.imread(filename)
        writer.append_data(image)
for filename in set(nfilenames):
    os.remove(filename)

with imageio.get_writer('2Dheatanalytical.gif', mode='I') as writer:
    for filename in afilenames:
        image = imageio.imread(filename)
        writer.append_data(image)
for filename in set(afilenames):
    os.remove(filename)

Heat Equation

Figure 1: \(\Omega=[0,1]\times[0,1]\) and \(f(z)=f_j(z)=\sin{(\pi x)}\sin{(\pi y)}\) \(\rightarrow\) \(\lambda_j=-2\pi^2\) \(u(x,y,t)=\sin{(\pi x)}\sin{(\pi y)}e^{-2\pi^2 t}\)