Spectral Method ODE

Let us have a look at the following initial value problem with linear operator L: $$L u(x)=f(x),\:\:\:\:\:\:\:\:\:x \in [x_0,x_1]\:\:\:\:\:\:\:\:\: u(x_0)=u_0\:\:\:\:\:\:\:\:\: u(x_1)=u_1$$ the spectral grid with N points is given by: $$x=-c\cos{(j\pi/(N-1))}+d,\:\:\:\:\:\:\:\:\:c:=\dfrac{x_1-x_0}{2}\:\:\:\:d:=\dfrac{x_1+x_0}{2}$$ The first derivative is given by the following matrix: $$D_{N-1,N-1}=(2(N-1)^2+1)/(6c),\:\:\:\:\:\:\:\:\:D_{0,0}=-(2(N-1)^2+1)/(6c)$$ $$D_{i,j}=-((x[i]-d)/c)/(1-((x[i]-d)/c)^2)/(2c)\:\:\:\:\:\:\:\:\:\:for\:i=j$$ $$D_{i,j}=c_i/c_j(-1)^{(i+j)}/(x[i]/c-x[j]/c)/c\:\:\:\:\:\:\:\:\:\:for\:i\neq j$$ with $c_i=2\:for\:i=\{0,N-1\}$ and $c_i=1$ if $i\neq \{0,N-1\}$.

Now starting with $D_{ij}$ any linear operator $L$ can be created using matrix multiplication.

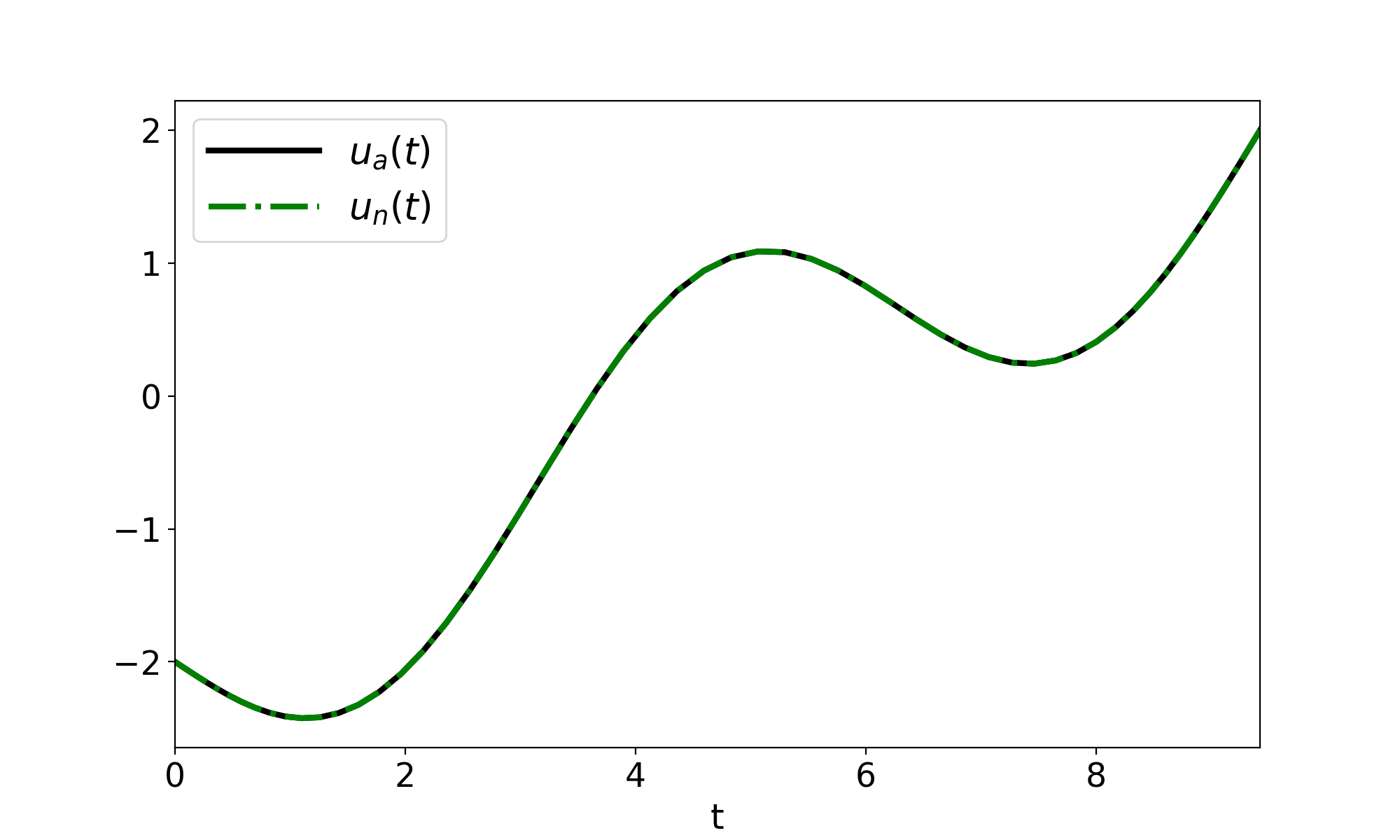
Figure 1: shows the comparison of the analytical solution with the numerical calculated result for the operator $L=\dfrac{d^2}{dx^2}$, $f=\sin{(x)}$ in $u\in [0,3 \pi]$ with $u(0)=-2$ and $u(3 \pi)=2$.

ODE

View Code

"""
The code below was written by https://github.com/DianaNtz and
is an implementation of a spectral ODE solver with dirichlet boundary condition.
"""

#import libraries
import numpy as np
import matplotlib.pyplot as plt

#setting up the grid
zmin=0
zmax=3*np.pi
N=64
z=np.linspace(zmin,zmax,N)

zz=np.zeros(N)
c=(zmax-zmin)/2
d=(zmax+zmin)/2
for j in range(0,N):

    zz[j]=-np.cos(j*np.pi/(N-1))*c+d
#first spectral derivative
Dz=np.zeros((N,N))
Dz[0][0]=-(2*(N-1)**2+1)/6
Dz[N-1][N-1]=(2*(N-1)**2+1)/6
for i in range(0,N):
    if(i==0 or i==N-1):
        ci=2
    else:
        ci=1
    for j in range(0,N):
        if(j==0 or j==N-1):
            cj=2
        else:
            cj=1
        if(i==j and i!=0 and i!=N-1):
           Dz[i][i]=-((zz[i]-d)/c)/(1-((zz[i]-d)/c)**2)*0.5
        if(i!=j):
          Dz[i][j]=ci/cj*(-1)**(i+j)/(zz[i]/c-zz[j]/c)

Dz=Dz/c

D2z=np.matmul(Dz,Dz)

#dirichlet boundary condition
b=np.sin(zz)
b[0]=-2
b[N-1]=2

for j in range(0,N):
        if(j==0):
           D2z[0][j]=1
        else:
           D2z[0][j]=0

        if(j==N-1):
            D2z[N-1][j]=1
        else:
            D2z[N-1][j]=0

#solving linear system
un=np.linalg.solve(D2z,b)
ua=-np.sin(zz)+4/(3*np.pi)*zz-2
ax1 = plt.subplots(1, sharex=True, figsize=(10,6))
plt.plot(zz,ua,color='black',linestyle='-',linewidth=3,label="$u_a(t)$")
plt.plot(zz,un,color='green',linestyle='-.',linewidth=3,label="$u_n(t)$")
plt.xlabel("t",fontsize=18)
plt.ylabel(r' ',fontsize=18,labelpad=20).set_rotation(0)
plt.xlim([zmin,zmax])
plt.xticks(fontsize= 17)
plt.yticks(fontsize= 17)
plt.legend(loc=2,fontsize=19,handlelength=3)
plt.savefig("spectral1d.png",dpi=200)
plt.show()

References
[1] https://www.sciencedirect.com/science/article/pii/S0307904X12005938

Spectral Method ODE

Figure 1: shows the comparison of the analytical solution with the numerical calculated result for the operator \(L=\dfrac{d^2}{dx^2}\), \(f=\sin{(x)}\) in \(u\in [0,3 \pi]\) with \(u(0)=-2\) and \(u(3 \pi)=2\).