Brill Data
Dieter Brill studied 1959 axisymmetric space times:
$$\gamma_{ij}^B=\Psi^4\begin{pmatrix}
e^{2q} & 0 & 0\\
0 & e^{2q}& 0\\
0 & 0 &\rho^2
\end{pmatrix},\:\:\:\:i\in\{\rho,z,\phi\}$$
setting the Ricci scalar of \(\gamma_{ij}^B\) to zero one finds for \(\psi\):
$$R_B=0\Rightarrow L_B\psi=0$$
$$L_B=(\partial_z^2+\partial_\rho^2+\dfrac{1}{\rho}\partial_\rho+\frac{1}{4}\partial_z^2q+\frac{1}{4}\partial_\rho^2q)$$
The Holz data considers a source function \(q\):
$$
q(\rho,z)=A_B\rho^2e^{-\rho^2-z^2}
$$
In general \(q\) can be any function that satisfies:
$$
q|_{\rho=0}=0,\:\:\:\partial^n_\rho q|_{\rho=0}=0\:\:\:q|_{r\rightarrow \infty}=\mathcal{O}(r^{-2})
$$
for odd n. The boundary conditions are:
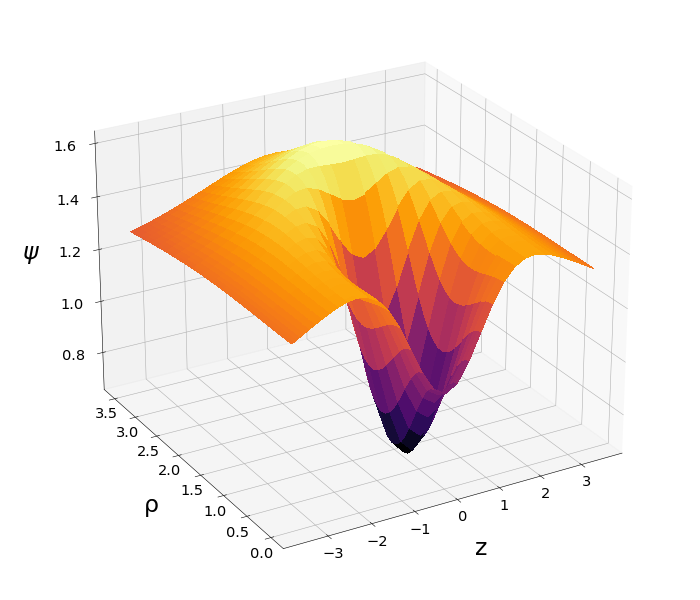
Figure 1: Conformal factor for an Brill wave with Holz data and amplitude \(A_B=10\).
$$\dfrac{\partial}{\partial \rho}\psi=0\:for\:\rho=0,\:\:\:\:\:\:\:\:(\rho^2+z^2)\dfrac{\partial}{\partial \rho}\psi+\rho\psi=\rho\:for\:\rho=\rho_{max},\:\:\:\:\:\:\:\:(\rho^2+z^2)\dfrac{\partial}{\partial z}\psi+z\psi=z\:for\:z=\{z_{min},z_{max}\}$$
This linear equation can be solved with spectral methods.
References
[1] https://arxiv.org/abs/gr-qc/9809004
[1] https://arxiv.org/abs/gr-qc/9809004
"""The code below was written by @author: https://github.com/DianaNtz and
solves Brill Wave initial data via spectral methods. """
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
#create grid
def Cheb_grid_and_D(xmin,xmax,Nx):
x=np.zeros(Nx)
cx=(xmax-xmin)/2
dx=(xmax+xmin)/2
for j in range(0,Nx):
x[j]=-np.cos(j*np.pi/(Nx-1))*cx+dx
Dx=np.zeros((Nx,Nx))
Dx[0][0]=-(2*(Nx-1)**2+1)/6
Dx[Nx-1][Nx-1]=(2*(Nx-1)**2+1)/6
for i in range(0,Nx):
if(i==0 or i==Nx-1):
ci=2
else:
ci=1
for j in range(0,Nx):
if(j==0 or j==Nx-1):
cj=2
else:
cj=1
if(i==j and i!=0 and i!=Nx-1):
Dx[i][i]=-((x[i]-dx)/cx)/(1-((x[i]-dx)/cx)**2)*0.5
if(i!=j):
Dx[i][j]=ci/cj*(-1)**(i+j)/(x[i]/cx-x[j]/cx)
Dx=Dx/cx
return x,Dx,np.dot(Dx,Dx)
#Holz data
sigma_rho=1
sigma_z=1
Amp=10
rho0=0.0
z0=0.0
def fq(rho,z):
return Amp*(rho)**2*np.exp(-(rho-rho0)**2/sigma_rho**2-(z-z0)**2/sigma_z**2)
#Initial values
Nz=41
Nrho=51
zmin=-3.5
zmax=3.5
rhomax=3.5
rhomin=0.0
rho,Drho,D2rho=Cheb_grid_and_D(rhomin,rhomax,Nrho)
z,Dz,D2z=Cheb_grid_and_D(zmin,zmax,Nz)
q=np.zeros(Nrho*Nz)
rhov=np.zeros(Nrho*Nz)
for j in range(0,Nrho):
for i in range(0,Nz):
q[i+j*Nz]=fq(rho[j],z[i])
rhov[i+j*Nz]=rho[j]
#create linear operator L
dz=np.kron(np.identity((Nrho)),Dz)
d2z=np.kron(np.identity((Nrho)),D2z)
drho=np.kron(Drho,np.identity((Nz)))
d2rho=np.kron(D2rho,np.identity((Nz)))
d2rhoq=np.dot(d2rho,q)
d2zq=np.dot(d2z,q)
fneu=rhov**2*(d2rhoq+d2zq)/4
c1rho=np.zeros([Nrho*Nz,Nrho*Nz], dtype='double')
c2rho=np.zeros([Nrho*Nz,Nrho*Nz], dtype='double')
c2z=np.zeros([Nrho*Nz,Nrho*Nz], dtype='double')
cf=np.zeros([Nrho*Nz,Nrho*Nz], dtype='double')
b1rho=np.zeros([Nrho*Nz,Nrho*Nz], dtype='double')
b2rho=np.zeros([Nrho*Nz,Nrho*Nz], dtype='double')
b2z=np.zeros([Nrho*Nz,Nrho*Nz], dtype='double')
for j in range(0,Nrho):
for i in range(0,Nz):
cf[i+j*Nz][i+j*Nz]=fneu[i+j*Nz]
c1rho[i+j*Nz][i+j*Nz]=rhov[i+j*Nz]
c2rho[i+j*Nz][i+j*Nz]=rhov[i+j*Nz]**2
c2z[i+j*Nz][i+j*Nz]=rhov[i+j*Nz]**2
b1rho[i+j*Nz][i+j*Nz]=(rho[j]**2+z[i]**2)
b2rho[i+j*Nz][i+j*Nz]=rho[j]
b2z[i+j*Nz][i+j*Nz]=z[i]
boundrho=np.matmul(b1rho,drho)+b2rho
boundz=np.matmul(b1rho,dz)+b2z
L=np.matmul(c1rho,drho)+np.matmul(c2rho,d2rho)+np.matmul(c2z,d2z)+cf
#setting boundaries
b=np.zeros(Nrho*Nz)
for j in range(0,Nrho):
for i in range(0,Nz):
if(i==0):
b[i+j*Nz]=z[0]
if(i==Nz-1):
b[i+j*Nz]=z[-1]
if(j==Nrho-1):
b[i+j*Nz]=rho[-1]
for k in range(0,Nrho*Nz):
if(k%Nz==0):
#z bei 0
L[k]=boundz[k]
if(k < Nz ):
L[k]=drho[k]
#rho bei 0
if(k%Nz==Nz-1):
L[k]=boundz[k]
#z bei Nz
if(k>=Nrho*Nz-Nz):
L[k]=boundrho[k]
#rho bei Nrho
#solve linear system
solution=np.linalg.solve(L,b)
print(np.linalg.matrix_rank(L,tol=0.000000000000001))
print(Nrho*Nz)
so=solution.reshape(Nrho,Nz)
#plotting results
zz,rhorho= np.meshgrid(z, rho)
fig = plt.figure(figsize=(14,12))
axx = plt.axes(projection='3d')
axx.plot_surface(zz, rhorho, so,cmap=cm.inferno,antialiased=False)
axx.view_init(azim=240,elev=25)
axx.set_xlabel('z', labelpad=30,fontsize=34)
axx.set_ylabel("ρ",labelpad=30,fontsize=34)
axx.zaxis.set_rotate_label(False)
axx.set_zlabel('$\psi$',labelpad=40,fontsize=34,rotation=0)
axx.zaxis.set_tick_params(labelsize=21,pad=18)
axx.yaxis.set_tick_params(labelsize=21)
axx.xaxis.set_tick_params(labelsize=21)
fig.subplots_adjust(left=0, right=1, bottom=0, top=1)
filename ="psi12.png"
plt.savefig(filename,dpi=50)
plt.show()