2D Crank Nicolson Method
The 2 dimensional Schrödinger equation is given by:
$$i\hbar\dfrac{\partial}{\partial t}\psi(x,y,t)=\Big(-\dfrac{\:\:\:\hbar^2}{2m}\Delta+V(x,y)\Big)\psi(x,y,t)$$
where the Laplace operator \(\Delta\) is:
$$\dfrac{\partial^2}{\partial x^2}+\dfrac{\partial^2}{\partial y^2}$$
Just like in the 1 dimensional case we want to discretize the above system in the common Crank Nicolson way:
$$\dfrac{u_{i,j}^{n+1}-u_{i,j}^n}{\Delta t}=\dfrac{1}{2}(F_{i,j}^{n+1}+F_{i,j}^n)$$
Therefore we replace the potential by:
$$V(x,y)\psi(x,y,t)\:\Rightarrow\:V_{i,j}\psi_{i,j}$$
the time derivation by:
$$\dfrac{\partial}{\partial t}\psi(x,y,t)\:\Rightarrow\:\dfrac{\psi_{i,j}^{n+1}-\psi_{i,j}^n}{\Delta t}$$
and the second order space derivations by:
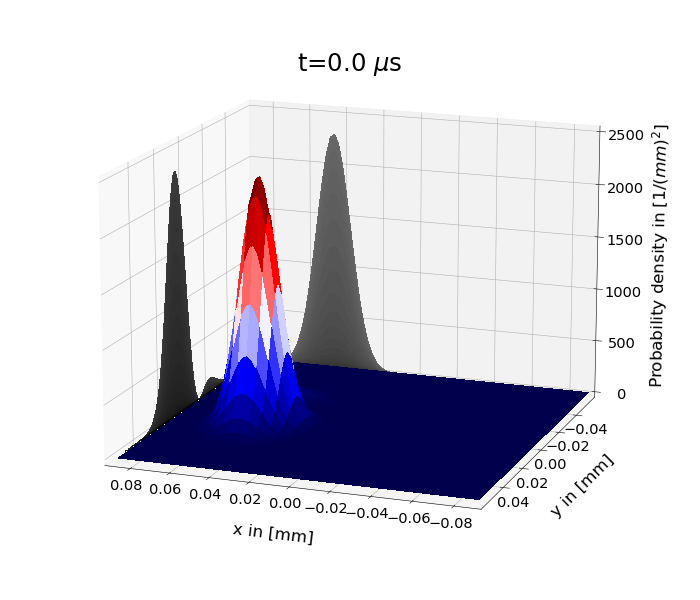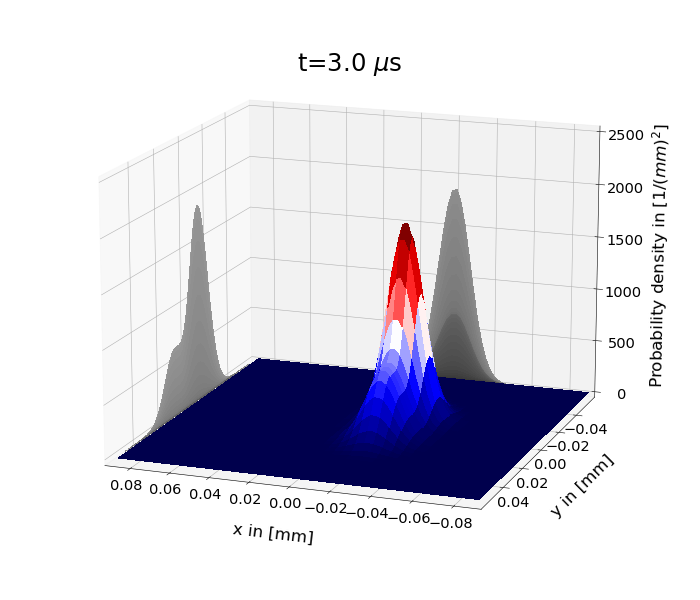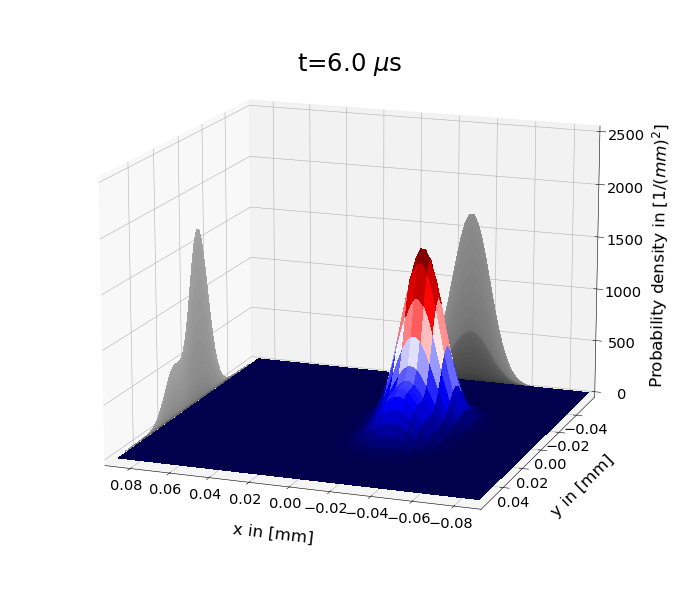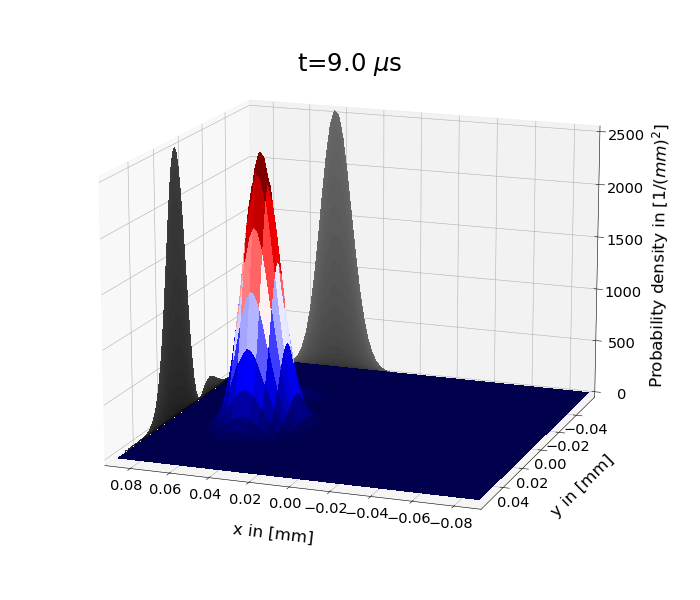
Figure 1: shows the time evolution of the probability density under the 2D harmonic oscillator Hamiltonian for \(\psi(x,y,0)=\psi_s(y,0)\psi_\alpha (x,0)\). \(\psi_s\) is the superposition of the two lowest eigenstates and \(\psi_\alpha \) a coherent state. One has set \(m=m_e\) and \(\omega_x=\omega_y=110\cdot 2\pi\) kHz.
$$\dfrac{\partial^2}{\partial x^2}\psi (x,y,t)\:\Rightarrow\:\dfrac{1}{2(\Delta x)^2}\Big((\psi_{i+1,j}^{n}-2\psi_{i,j}^{n}+\psi_{i-1,j}^{n})+(\psi_{i+1,j}^{n+1}-2\psi_{i,j}^{n+1}+\psi_{i-1,j}^{n+1})\Big)$$
$$\dfrac{\partial^2}{\partial y^2}\psi (x,y,t)\:\Rightarrow\:\dfrac{1}{2(\Delta y)^2}\Big((\psi_{i,j+1}^{n}-2\psi_{i,j}^{n}+\psi_{i,j-1}^{n})+(\psi_{i,j+1}^{n+1}-2\psi_{i,j}^{n+1}+\psi_{i,j-1}^{n+1})\Big)$$
Plugging in the above expressions in the Schrödinger equation leads us to:
$$\psi_{i,j}^{n+1}-\dfrac{\hbar i \Delta t}{4m(\Delta x)^2}(\psi_{i+1,j}^{n+1}-2\psi_{i,j}^{n+1}+\psi_{i-1,j}^{n+1})-\dfrac{\hbar i \Delta t}{4m(\Delta y)^2}(\psi_{i,j+1}^{n+1}-2\psi_{i,j}^{n+1}+\psi_{i,j-1}^{n+1})+\frac{\Delta t}{2\hbar}V_{i,j}\Psi_{i,j}^{n+1}$$
$$=\psi_{i,j}^{n}+\dfrac{\hbar i \Delta t}{4m(\Delta x)^2}(\psi_{i+1,j}^{n}-2\psi_{i,j}^{n}+\psi_{i-1,j}^{n})+\dfrac{\hbar i \Delta t}{4m(\Delta y)^2}(\psi_{i,j+1}^{n}-2\psi_{i,j}^{n}+\psi_{i,j-1}^{n})-\frac{\Delta t}{2\hbar}V_{i,j}\Psi_{i,j}^{n}$$
this can be written in matrix form \(A\psi^{n+1}=B\psi^n\) the following way:
$$\begin{pmatrix}
A_0&D&{} &{}&{}\\
D&A_1&D&{}&{}\\
{}&D&A_2&D&{}\\
{}&{}&D&\ddots&\ddots\\
{}&{}&{}&{\ddots}&A_{N-1}\\
\end{pmatrix}\begin{pmatrix}
\psi_0^{n+1}\\
\psi_1^{n+1}\\
\psi_2^{n+1}\\
\vdots\\
\psi_{N-1}^{n+1}\\
\end{pmatrix}=\begin{pmatrix}
\:\:\:B_0&-D&{} &{}&{}\\
-D&\:\:\:B_1&-D&{}&{}\\
{}&-D&\:\:\:B_2&-D&{}\\
{}&{}&-D&\ddots&\ddots\\
{}&{}&{}&{\ddots}&\:\:\:B_{N-1}\\
\end{pmatrix}\begin{pmatrix}
\psi_0^{n}\\
\psi_1^{n}\\
\psi_2^{n}\\
\vdots\\
\psi_{N-1}^{n}\\
\end{pmatrix}$$
Note that the system above is written in blockmatrix form and we have set the number of gridpoints in x and y direction equal to \(N\).
The explicit form of \( \psi_j^n\) and \(D\) is given by:
$$\psi_j^n:=\begin{pmatrix}
\psi_{0,j}^{n}\\
\psi_{1,j}^{n}\\
\psi_{2,j}^{n}\\
\vdots\\
\psi_{N-1,j}^{n}\\
\end{pmatrix},\:\:\:\:\:\:\:\:\:\:\:\:D:=\begin{pmatrix}
-a_x&{}&{} &{}&{}\\
{}&-a_x&{}&{}&{}\\
{}&{}&-a_x&{}&{}\\
{}&{}&{}&\ddots&{}\\
{}&{}&{}&{}&-a_x\\
\end{pmatrix}$$
The blockmatrices \(A_j\) and \(B_j\) are:
$$A_j:=\begin{pmatrix}
\:\:\:A_{0,j}&-a_y&{} &{}&{}\\
-a_y&\:\:\:A_{1,j}&-a_y&{}&{}\\
{}&-a_y&\:\:\:A_{2,j}&-a_y&{}\\
{}&{}&-a_y&\ddots&\ddots\\
{}&{}&{}&{\ddots}&\:\:\:A_{N-1,j}\\
\end{pmatrix},\:\:\:\:\:\:\:\:\:\:\:\:B_j:=\begin{pmatrix}
B_{0,j}&a_y&{} &{}&{}\\
a_y&B_{1,j}&a_y&{}&{}\\
{}&a_y&B_{2,j}&a_y&{}\\
{}&{}&a_y&\ddots&\ddots\\
{}&{}&{}&{\ddots}&B_{N-1,j}\\
\end{pmatrix}$$
Note that we have defined the complex coefficients as:
$$a_x:=\dfrac{\hbar i \Delta t}{4m(\Delta x)^2},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:a_y:=\dfrac{\hbar i \Delta t}{4m(\Delta y)^2}$$
and the diagonal entries of the matrices \(A\) and \(B\) as:
$$A_{i,j}:=1+2a_x+2a_y+\dfrac{i\Delta t}{2\hbar}V_{i,j},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:B_{i,j}:=1-2a_x-2a_y-\dfrac{i\Delta t}{2\hbar}V_{i,j}$$
In order to solve the system one can again invert the matrix \(A\). However for a block tridiagonal matrix this can be done blockwise like in [1].
The diagonal blockmatrix entries of \(A^{-1}\) are therefore given by:
$$(A^{-1})_{n,n}=[A_n-X_n-Y_n]^{-1}$$
where \(X_n\) and \(Y_n\) are given by:
$$X_n:=\begin{cases}
0,& \text{if } n=N-1\\
D[A_{n+1}-X_{n+1}]^{-1}D,& \text{if } 0\leq n < N-1
\end{cases},\:\:\:\:\:\:\:\:\:Y_n:=\begin{cases}
0,& \text{if } n=0\\
D[A_{n-1}-Y_{n-1}]^{-1}D,& \text{if } 0 < n \leq N-1
\end{cases}$$
the off diagonal entries are:
$$(A^{-1})_{m,n}=\begin{cases}
-(A_m-X_m)^{-1}D(A^{-1})_{m-1,n},& \text{if } m > n\\
-(A_m-Y_m)^{-1}D(A^{-1})_{m+1,n},& \text{if } m < n
\end{cases}$$
References
[1] http://dx.doi.org/10.1088/1749-4699/5/1/014009
[2] https://en.wikipedia.org/wiki/Crank%E2%80%93Nicolson_method
[1] http://dx.doi.org/10.1088/1749-4699/5/1/014009
[2] https://en.wikipedia.org/wiki/Crank%E2%80%93Nicolson_method
"""
The code below was written by @author: https://github.com/DianaNtz and is an
implementation of the 2D Crank Nicolson method. It solves in particular the
Schrödinger equation for the quantum harmonic oscillator. For more details on
the code requirements and licences see
https://github.com/DianaNtz/2D-Crank-Nicolson-Method.
"""
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
from matplotlib import cm
import os
import imageio
filenames = []
#some initial values
hbar = 1.0545718e-34
mass = 9.11e-31 #mass electron
wx = 110*2*np.pi*1000 #freuquency in Hz
wy = 110*2*np.pi*1000 #freuquency in Hz
x0 = np.sqrt(hbar / (wx * mass)) #in m
y0 = np.sqrt(hbar / (wy * mass)) #in m
dt = 1e-8 #dt in s
tfinal = 2*np.pi/wx #final time in s
time_steps = int(np.round(tfinal/dt))
t = 0.0 #initial time
N = 80 #grid points
xmax = 6.9 * x0
xmin = -6.9 * x0
ymax = 4.6 * y0
ymin = -4.6 * y0
dx = (xmax - xmin) / ((N - 1))
dy = (ymax - ymin) / ((N - 1))
xn=np.linspace(-N/2,N/2-1,N)
x=xn*dx
yn=np.linspace(-N/2,N/2-1,N)
y=yn*dy
X, Y = np.meshgrid(x, y)
Z=np.empty([N, N], dtype='double')
ax = (1j * dt / hbar) * (hbar**2 / (mass * dx**2))*0.25
ay = (1j * dt / hbar) * (hbar**2 / (mass * dy**2))*0.25
Vy=0.5*wy**2*y**2*mass #1D potential for y dimension
Vx=0.5*wx**2*x**2*mass #1D potential for x dimension
#1D wave functions for x dimension
absalphax=2.5
psicox=np.exp(-((x-x0*np.sqrt(2)*absalphax)/x0)**2/2)
normcox=np.sum(psicox*np.conjugate(psicox))*dx
psicox=psicox/np.sqrt(normcox)
#1D wave functions for y dimension
psi0y=np.exp(-((y)/y0)**2/2)
norm0y=np.sum(psi0y*np.conjugate(psi0y))*dy
psi0y=psi0y/np.sqrt(norm0y)
psi1y=np.exp(-((y)/y0)**2/2)*2*y/y0
norm1y=np.sum(psi1y*np.conjugate(psi1y))*dy
psi1y=psi1y/np.sqrt(norm1y)
#setting up 2D arrays for potential and wave function
V2D=np.empty([N, N], dtype=complex)
Psi2D=np.empty([N, N], dtype=complex)
a2D=np.empty([N, N], dtype=complex)
b2D=np.empty([N, N], dtype=complex)
for i in range(0,N):
for j in range(0,N):
V2D[i][j]=Vx[i]+Vy[j]
Psi2D[i][j]=psicox[i]*1/np.sqrt(2)*(psi0y[j]+psi1y[j])
a2D[i][j]=1.0 + 2.0 * ax + 2.0 * ay + 0.5*1j * dt / hbar * V2D[i][j]
b2D[i][j]=1.0 - 2.0 * ax - 2.0 * ay - 0.5*1j * dt / hbar * V2D[i][j]
#calculating initial probability density for x and y direction
abx0=np.empty(N,dtype=object)
aby0=np.empty(N,dtype=object)
for j in range(0,N):
abx0[j]=np.sum(np.real(Psi2D[j,:]*np.conjugate(Psi2D[j,:])))*dy
for i in range(0,N):
aby0[i]=np.sum(np.real(Psi2D[:,i]*np.conjugate(Psi2D[:,i])))*dx
#initialising block matrices A and B
AList=np.empty(N, dtype=object)
BList=np.empty(N, dtype=object)
for k in range(0,N):
A=np.identity(N)*0.0*1j
B=np.identity(N)*0.0*1j
for i in range(0,N):
for j in range(0,N):
if (j==i):
A[i][j]=a2D[k][j]
B[i][j]=b2D[k][j]
elif (j==i+1):
A[i][j]=-ay
B[i][j]=ay
elif (j==i-1):
A[i][j]=-ay
B[i][j]=ay
else:
A[i][j]=0.0
B[i][j]=0.0
AList[k]=A
BList[k]=B
#invert matrix A blockwise with X and Y
XList=np.empty(N, dtype=object)
YList=np.empty(N, dtype=object)
for k in range(N-1,-1,-1):
XList[k]=np.identity(N)*0.0*1j
if(k==N-1):
XList[k]=np.identity(N)*0.0*1j
else:
XList[k]=np.linalg.inv(AList[k+1]-XList[k+1])*ax**2
for k in range(0,N):
YList[k]=np.identity(N)*0.0*1j
if(k==0):
YList[k]=np.identity(N)*0.0*1j
else:
YList[k]=np.linalg.inv(AList[k-1]-YList[k-1])*ax**2
Ainv=np.empty([N, N], dtype=object)
for j in range(0,N):
for i in range(0,N):
if(i==j):
Ainv[i][j]=np.linalg.inv(AList[i]-XList[i]-YList[i])
elif(i > j):
Ainv[i][j]=np.dot(ax*np.linalg.inv(AList[i]-XList[i]),Ainv[i-1][j])
for j in range(0,N):
for i in range(N-1,-1,-1):
if(i < j):
Ainv[i][j]=np.dot(ax*np.linalg.inv(AList[i]-YList[i]),Ainv[i+1][j])
#starting loop for time propagation
BmalPsi2D=np.empty([N, N], dtype=complex)
for p in range(0,time_steps+1):
if(p%100==0):
print(p)
#multipy matrix B with psi
for k in range(0,N):
if(k==0):
BmalPsi2D[k]=BList[k].dot(Psi2D[k])+ax*(Psi2D[k+1])
elif (k==N-1):
BmalPsi2D[k]=BList[k].dot(Psi2D[k])+ax*(Psi2D[k-1])
else:
BmalPsi2D[k]=ax*(Psi2D[k+1])+BList[k].dot(Psi2D[k])+ax*(Psi2D[k-1])
#multipy inverse of A with BmalPsi2D
for j in range(0,N):
ka=0.0*1j
for i in range(0,N):
ka=Ainv[j][i].dot(BmalPsi2D[i])+ka
Psi2D[j]=ka
if(p%10==0):
print(p)
#creating a 2D probability density gif animation with imageio
fig = plt.figure(figsize=(14,12))
axx = plt.axes(projection='3d')
for ii in range(0,N):
for jj in range(0,N):
Z[jj][ii]=np.real(Psi2D[ii][jj]*np.conjugate(Psi2D[ii][jj]))
axx.plot_surface(X*10**(3), Y*10**(3), Z/(10**6),cmap=cm.seismic,
antialiased=False)
axx.contourf(X*10**(3), Y*10**(3), Z/(10**6),100, zdir='x',
offset=xmax*10**3,cmap=cm.binary)
axx.contourf(X*10**(3), Y*10**(3), Z/(10**6),100, zdir='y',
offset=ymin*10**3,cmap=cm.binary)
axx.view_init(azim=110,elev=15)
axx.set_xlabel('x in [mm]', labelpad=30,fontsize=24)
axx.set_ylabel('y in [mm]',labelpad=30,fontsize=24)
axx.set_ylim(ymin*10**3,ymax*10**3)
axx.set_xlim(xmin*10**3,xmax*10**3)
axx.set_zlabel('Probability density in [1/$(mm)^2$]',labelpad=40,fontsize=24)
stringtitle="t=".__add__(str(round(t*10**(6),1))).__add__(" $\mu$s")
plt.title(stringtitle,fontsize=35,x=0.5, y=0.95)
axx.set_zlim(0, 2500)
axx.zaxis.set_tick_params(labelsize=21,pad=18)
axx.yaxis.set_tick_params(labelsize=21)
axx.xaxis.set_tick_params(labelsize=21)
fig.subplots_adjust(left=0, right=1, bottom=0, top=1)
filename ='bla{0:.0f}.png'.format(p/10)
filenames.append(filename)
plt.savefig(filename,dpi=50)
plt.close()
t=t+dt
with imageio.get_writer('2DCN.gif', mode='I') as writer:
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
for filename in set(filenames):
os.remove(filename)
#calculating final probability density for x and y direction
abx=np.empty(N,dtype=object)
aby=np.empty(N,dtype=object)
for j in range(0,N):
abx[j]=np.sum(np.real(Psi2D[j,:]*np.conjugate(Psi2D[j,:])))*dy
for i in range(0,N):
aby[i]=np.sum(np.real(Psi2D[:,i]*np.conjugate(Psi2D[:,i])))*dx
#plotting initial vs final probability density for x and y direction
fig, ax1 = plt.subplots(1, sharex=True, figsize=(10,5))
plt.plot(x/10**-3,abx0/10**(3), color='g',linestyle='-',
linewidth=3.0,label = "$|\psi(x,t_0)|^2$")
plt.plot(x/10**-3,abx/10**(3), color='r',linestyle='-.',
linewidth=3.0,label = "$|\psi(x,t_{fianl})|^2$")
plt.xlabel("Position in [mm]",rotation=0,fontsize=15)
plt.ylabel(r'Probability density [1/mm]',fontsize=15)
plt.xticks(fontsize= 14)
plt.yticks(fontsize= 14)
plt.xlim([xmin*10**3,xmax*10**3])
plt.ylim([0,70])
plt.legend(loc=2,fontsize=20)
plt.savefig('x2D.png',dpi=120)
plt.show()
fig, ax1 = plt.subplots(1, sharex=True, figsize=(10,5))
plt.plot(y/10**-3,aby0/10**(3), color='b',linestyle='-',
linewidth=3.0,label = "$|\psi(y,t_0)|^2$")
plt.plot(y/10**-3,aby/10**(3), color='r',linestyle='-.',
linewidth=3.0,label = "$|\psi(y,t_{fianl})|^2$")
plt.xlabel("Position in [mm]",rotation=0,fontsize=15)
plt.ylabel(r'Probability density [1/mm]',fontsize=15)
plt.xticks(fontsize= 14)
plt.yticks(fontsize= 14)
plt.xlim([ymin*10**3,ymax*10**3])
plt.ylim([0,80])
plt.legend(loc=2,fontsize=20)
plt.savefig('y2D.png',dpi=120)
plt.show()