1D Crank Nicolson Method

The Crank Nicolson algorithm is a finite difference method and can be interpreted as a combination of the forward and backward Euler method. It is famous for solving the heat equation numerically but any equation of the form: $$\dot{u}(z,t)=F(z,t,u(z,t),u'(z,t),u''(z,t))$$ can be solved with the Crank Nicolson method. A well known example of this type is the Schrödinger equation: $$i\hbar\dfrac{\partial}{\partial t}\psi(z,t)=\Big(-\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{\partial z^2}+V(z)\Big)\psi(z,t)$$ The time evolution for a small amount of $d t$ is: $$\Psi(z,t+d t)=\hat{U}\psi(z,t),\:\:\:\:\:\:\:\:\:\:\:\hat{U}:=e^{-i\hat{H}dt/\hbar},\:\:\:\:\:\:\:\:\:\:\:\hat{H}:=-\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{\partial z^2}+V(z)$$ that is equivalent to: $$e^{i\hat{H}d t/(2\hbar)}\Psi(z,t+d t)=e^{-i\hat{H}d t/(2\hbar)}\psi(z,t)$$ This can be Taylor expanded to: $$\Big(1+\dfrac{i}{2\hbar}\hat{H} dt\Big)\psi(z,t+dt)= \Big(1-\dfrac{i}{2\hbar}\hat{H}dt\Big)\psi(z,t)$$ Let now i be the space index and n the time index of our discretized system, then we obtain for the derivations: $$\dfrac{\partial}{\partial t}\psi(z,t)\:\:\Rightarrow\:\:\dfrac{\psi_i^{n+1}-\psi_i^n}{\Delta t},\:\:\:\:\:\dfrac{\partial^2}{\partial z^2}\psi (z,t)\:\:\Rightarrow\:\:\dfrac{\psi_{i+1}^{n}-2\psi_{i}^{n}+\psi_{i-1}^{n}}{(\Delta z)^2}$$ So the discretized form of the equation above reads: $$\Big(1+\dfrac{i}{2\hbar}H_i \Delta t\Big)\psi_i^{n+1}= \Big(1-\dfrac{i}{2\hbar}H_i\Delta t\Big)\psi_i^n,\:\:\:\:\:\:\:\:\:\:\:\:H_i\Psi_i^n:=-\dfrac{\hbar^2}{2m}\dfrac{\psi_{i+1}^{n}-2\psi_{i}^{n}+\psi_{i-1}^{n}}{(\Delta z)^2}+V_i\Psi_i^n$$ Note that the equation is now in the standard half forward Euler and half backward Euler form, which is characteristic for the Crank Nicolson method: $$\dfrac{u_i^{n+1}-u_i^n}{\Delta t}=\dfrac{1}{2}(F_i^{n+1}+F_i^n)$$ This system can be written in matrix form as: $$A \psi^{n+1}=B \psi^{n}$$ The matrix $A$ is given by: $$A=I+\dfrac{i}{2\hbar}\Delta t\begin{pmatrix} V_1&{}&{} &{}&{}\\ {}&V_2&{}&{}&{}\\ {}&{}&V_3&{}&{}\\ {}&{}&{}&{\ddots}&{}\\ {}&{}&{}&{}&{V_n}\\ \end{pmatrix}-\dfrac{i}{2\hbar}\Delta t\dfrac{\hbar^2}{2m(\Delta z)^2}\begin{pmatrix} -2&\:\:\:1&{} &{}&{}\\ \:\:\:1&-2&\:\:\:1&{}&{}\\ {}&\:\:\:1&-2&\:\:\:1&{}\\ {}&{}&\:\:\:1&\ddots&\ddots\\ {}&{}&{}&{\ddots}&\ddots\\ \end{pmatrix}$$ $I$ is defined as identity matrix here. For the matrix $B$ one only needs to change the sign of $\Delta t$ in matrix $A$. So in order to solve the Schrödinger equation we need to solve the system $A \psi^{n+1}=B \psi^{n}$, this can be done in several ways, one is to simply invert matrix $A$: $$\psi^{n+1}=A^{-1}B \psi^{n}$$ Another way is to simply use an linear solver method such as np.linalg.solve. However, this would be really time consuming compared to the LU decomposition combined with tridiagonal solvers and even more time consuming compared to banded matrix solvers, which exploit the fact that most of our matrix entries are 0. In Python, scipy is providing most common solvers for that such as scipy.linalg.solve_banded, scipy.linalg.solve_triangular and scipy.linalg.lu. One thing especially worth mentioning is that the Crank Nicolson method described above can also be used to solve problems with a time depending potential $V(z,t)$, everything one has to do is to make the matrices $A$ and $B$ explicitly time dependent and update them for every timestep $\Delta t$.

Quantum Harmonic Oscillator

▼

In order to test the numerical solution we are going to have a look at the quantum harmonic oscillator:

$$\hat{H}=\dfrac{p_z^2}{2m}+\dfrac{m}{2}\omega_z^2z^2$$ that is the most standard system in physics partially due to its nice analytical solution, which can be derived from an algebraic approach discovered by Paul Dirac. The time independent Schrödinger equation is given by: $$(-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dz^2}+\dfrac{m}{2}\omega_z^2z^2)\psi(z)=E\psi(z)$$ Now one defines the so called creation and annihilation operators: $$\hat{a}^\dagger:=\dfrac{\omega_z m z- ip_z}{\sqrt{2\omega_z m \hbar}},\:\:\:\:\:\:\hat{a}:=\dfrac{\omega m z+ ip_z}{\sqrt{2\omega_z m \hbar}},\:\:\:\:\:\:with\:\:[\hat{a},\hat{a}^\dagger]=1$$ Note that the invers relation is given by: $$z=\sqrt{\dfrac{\hbar}{2\omega_z m}}(\hat{a}+\hat{a}^\dagger),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:p_z=-i\sqrt{\dfrac{\hbar\omega_z m}{2}}(\hat{a}-\hat{a}^\dagger)$$ The operators above can be written as: $$\hat{a}=\dfrac{1}{\sqrt{2}}(\dfrac{z}{z_0}+z_0\dfrac{d}{dz}),\:\:\:\:\:\:\:\:\:\:\:\hat{a}^\dagger=\dfrac{1}{\sqrt{2}}(\dfrac{z}{z_0}-z_0\dfrac{d}{dz}),\:\:\:\:\:\:with\:\:z_0=\sqrt{\dfrac{\hbar}{\omega_z m}}$$ The number operator is defined as $\hat{n}:=\hat{a}^\dagger \hat{a}$ and satisfies: $$[\hat{n},\hat{a}^\dagger]=\hat{a}^\dagger,\:\:\:\:\:\:\:\:\:\:\:[\hat{n},\hat{a}]=-\hat{a}$$ We therefore obtain for our Hamiltonian: $$H=\frac{1}{2}\hbar\omega_z(\hat{a}^\dagger \hat{a}+\hat{a} \hat{a}^\dagger)=\hbar\omega_z(\hat{a}^\dagger \hat{a}+\frac{1}{2})$$ The problem has now reduced to find the eigenfunctions of the number operator $\hat{n}$. Let $\psi_{\eta}$ be the eigenfunction of $\hat{n}$ with eigenvalue $\eta$. This eigenvalue can not be negative because: $$\eta\langle\psi_{\eta},\psi_{\eta}\rangle=\langle\psi_{\eta},\hat{a}^\dagger \hat{a}\psi_{\eta}\rangle=\langle \hat{a}\psi_{\eta},\hat{a} \psi_{\eta}\rangle\ge 0$$ So the smallest eigenvalue must be $\eta=0$, the eigenequation is given by: $$\hat{a}\psi_0=\dfrac{1}{\sqrt{2}}(\dfrac{z}{z_0}+z_0\dfrac{d}{dz})\psi_0=0$$ This equation is solved by: $$\psi_0(z)=\dfrac{1}{\sqrt{\sqrt{\pi}z_0}}\:e^{-\dfrac{1}{2}\big(\dfrac{z}{z_0}\big)^2}$$ The eigenfunction to the eigenvalue $\eta +1$ can be written as $\hat{a}^\dagger\psi_{\eta}$ because: $$\hat{n}\hat{a}^\dagger\psi_{\eta}=(\hat{a}^\dagger\hat{n}+\hat{a}^\dagger)\psi_{\eta}=(\eta+1)\hat{a}^\dagger\psi_{\eta}$$ For the norm one gets: $$\langle \hat{a}^\dagger\psi_{\eta},\hat{a}^\dagger\psi_{\eta}\rangle=\langle \psi_{\eta},\hat{a}\hat{a}^\dagger\psi_{\eta}\rangle=\langle \psi_{\eta},(\hat{a}^\dagger \hat{a}+1)\psi_{\eta}\rangle=(\eta+1)\langle\psi_{\eta},\psi_{\eta}\rangle$$ For normalised $\psi_{\eta}$ and $\psi_{\eta+1}$ it has to be: $$\hat{a}^\dagger\psi_{\eta}=\sqrt{\eta+1}\psi_{\eta+1}\:\:\Rightarrow\:\:\psi_{n}=\frac{1}{\sqrt{n}}\hat{a}^\dagger\psi_{n-1}=\frac{1}{\sqrt{n!}}(\hat{a}^\dagger)^n\psi_{0}$$ Furthermore note that $\hat{a}\psi_{\eta}$ is an eigenfunction to the eigenvalue $\eta-1$ since: $$\hat{n}\hat{a}\psi_{\eta}=(\hat{a}\hat{n}-\hat{a})\psi_{\eta}=(\eta-1)\hat{a}\psi_{\eta}$$ The norm is given by: $$\langle \hat{a}\psi_{\eta},\hat{a}\psi_{\eta} \rangle=\langle \psi_{\eta},\hat{a}^\dagger \hat{a}\psi_{\eta}\rangle=\eta\langle \psi_{\eta},\psi_{\eta} \rangle $$ such that: $$\hat{a}\psi_{\eta}=\sqrt{\eta}\psi_{\eta-1}$$ So with n $\in$ $\mathbb{N}$ we already found all of our eigenfunctions. Let us otherwise assume there was an eigenvalue $\eta=n+c$ with $0 < c<1$ and n $ \in $ $ \mathbb{N} $. One would obtain: $$\hat{n}\psi_{\eta}=(n+c)\psi_{\eta}\:\:\Rightarrow\:\:\hat{n}(\hat{a}^n\psi_{\eta})=c(\hat{a}^n\psi_{\eta})\:\:\Rightarrow\:\:\hat{n}(\hat{a}^{n+1}\psi_{\eta})=(c-1)(\hat{a}^{n+1}\psi_{\eta})$$ Therefore it would lead us to an eigenfunction with negative eigenvalue that we already excluded previously. So the solution for the quantum harmonic oscillator is: $$\psi_n(z)=\dfrac{1}{\sqrt{n!\sqrt{\pi}z_0}}(\hat{a}^\dagger)^ne^{-\dfrac{1}{2}\big(\dfrac{z}{z_0}\big)^2},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:E_n=\hbar\omega_z(n+\frac{1}{2})$$ The solution can also be written in terms of the Hermite polynomials as: $$\psi_n(z)=\dfrac{1}{\sqrt{2^nn!\sqrt{\pi}z_0}}e^{-\dfrac{1}{2}\big(\dfrac{z}{z_0}\big)^2}H_n(\dfrac{z}{z_0})$$ with: $$H_n(x)=e^{\frac{x^2}{2}}(\sqrt{2}a^\dagger)^ne^{-\frac{x^2}{2}}=e^{x^2}e^{-\frac{x^2}{2}}(x-\frac{d}{dx})^ne^{\frac{x^2}{2}}e^{-x^2}=(-1)^ne^{x^2}\frac{d^n}{dx^n}e^{-x^2}$$

Superposition State

▼

Now we want to check our numerical solution for the Crank Nicolson method against an analytical solution. So let us have a look at the time evolution for the first two eigenfunctions superposition state of the harmonic oscillator: $$\psi_s(z,0)=\dfrac{1}{\sqrt{2}}(\psi_0(z)+\psi_1(z))$$ The time evolution of an arbitrary initial state written in the eigenstate basis is: $$\psi(z,t)=\sum\limits_{n=0}^{\infty}c_ne^{-\frac{i}{\hbar}E_n t}\psi_n(z),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\psi(z,0)=\sum\limits_{n=0}^{\infty}c_n\psi_n(z)$$ So for our above initial state we get: $$\psi_s(z,t)=\dfrac{1}{\sqrt{2}}\Big(e^{-i\omega_z t/2}\psi_0(z)+e^{-3i\omega_z t/2}\psi_1(z)\Big)$$ with $\psi_n=\psi_n^\dagger$ we get for the probability density: $$|\psi_s (z,t)|^2=\frac{1}{2}(|\psi_0(z)|^2+|\psi_1(z)|^2)+\cos{(\omega_z t)}\psi_1 (z)\psi_0(z)$$

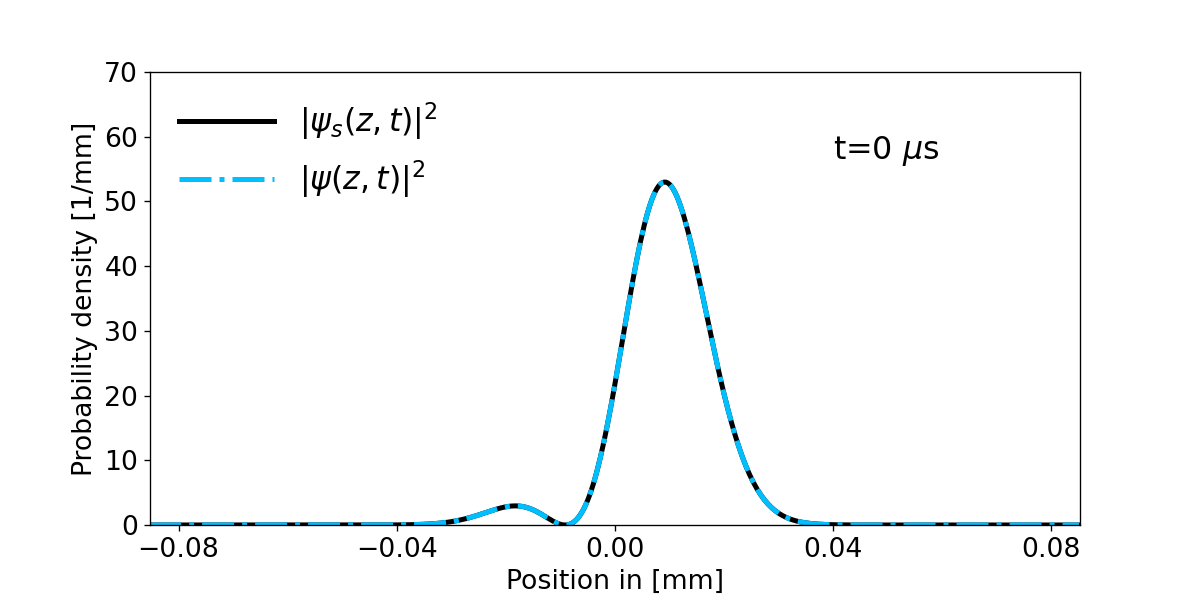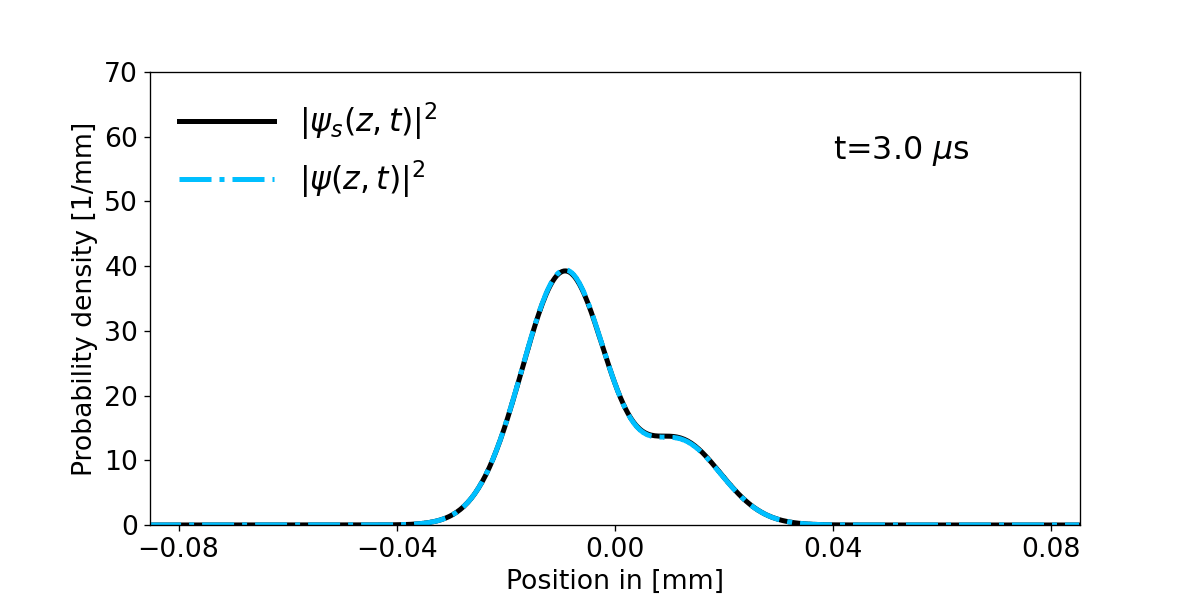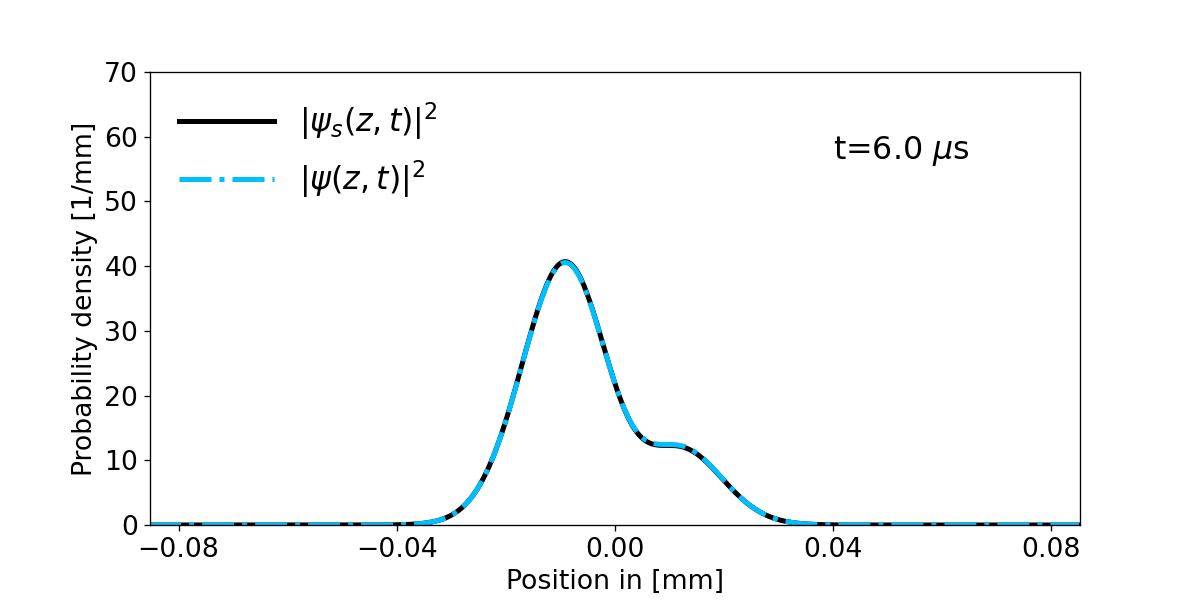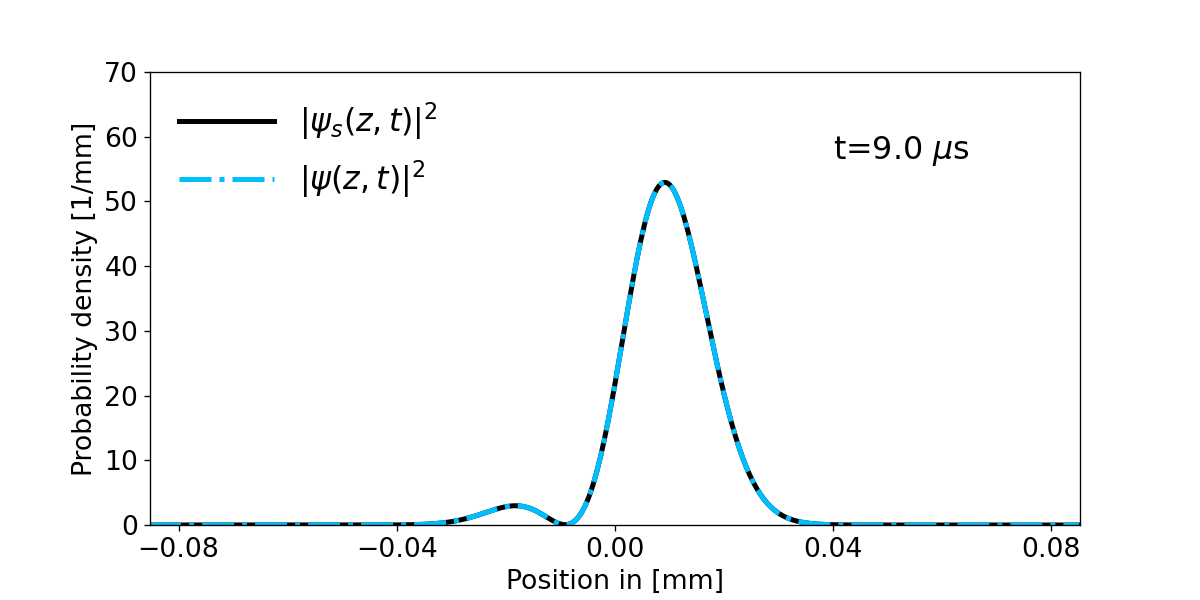
Figure 1: Shows the time evolution of the probability density for the initial superposition state $\psi_s(z,0)$ and compares its analytical solution $\psi_s(z,t)$ with the numerical calculated result from the above described Crank Nicolson method $\psi (z,t)$. Notice however that one has set $m=m_e$ and $\omega_z=110\cdot 2\pi$ kHz.

Coherent State

▼

Another interesting solution of the harmonic oscillator is the coherent state $\ket{\alpha}$ which is defined as: $$\hat{a}\ket{\alpha} =\alpha \ket{\alpha},\:\:\:\:\:\:\:\:\langle\hat{n}|\alpha\rangle=\bra{0}\frac{\hat{a}^n}{\sqrt{n!}}\ket{\alpha}=\frac{\alpha^n}{\sqrt{n!}}\braket{0}{\alpha}$$ Since the eigenstates build a basis of the Hilbert space we can write: $$\ket{\alpha}=C\sum_{n=0}^\infty\frac{\alpha^n}{\sqrt{n!}}\ket{n}=C\sum_{n=0}^\infty\frac{(\alpha \hat{a}^\dagger)^n}{n!}\ket{0},\:\:\:\:1=\langle \alpha|\alpha\rangle=C^2\sum_{n=0}^\infty \frac{|\alpha|^{2n}}{n!}=C^2e^{|\alpha|^2}\xrightarrow[]{}C=e^{-\frac{|\alpha|^2}{2}}$$ So the time evolution for a coherent state is given by: $$\langle z|\alpha\rangle=\Psi_\alpha (z,t)= e^{-\frac{|\alpha|^2}{2}}e^{-i\omega_z t/2}\sum_{n=0}^\infty\frac{(\alpha e^{-i\omega_z t})^n}{\sqrt{n!}}\Psi_n(z)$$ $$=\frac{1}{\sqrt{\sqrt{\pi}z_0}} e^{-\frac{|\alpha|^2}{2}}e^{-i\omega_z t/2}e^{-\frac{1}{2}(z/z_0)^2}\sum_{n=0}^\infty\frac{(\alpha/\sqrt{2} e^{-i\omega_z t})^n}{n!}H_n(z/z_0)$$ $$=\frac{1}{\sqrt{\sqrt{\pi}z_0}} e^{-\frac{|\alpha|^2}{2}}e^{-i\omega_z t/2}e^{-\frac{1}{2}(z/z_0)^2}e^{2(\alpha/\sqrt{2} e^{-i\omega_z t})z/z_0}e^{-(\alpha/\sqrt{2} e^{-i\omega_z t})^2}$$ Where we denoted with $H_n$ the Hermite polynomials and used the formula: $$e^{2ax-a^2}=\sum_{n=0}^\infty\frac{a^n}{n!}H_n(x)$$ If we now sum up the last three exponents of the equation above we obtain: $$-\frac{1}{2}((\alpha e^{-i\omega_z t})^2-2\sqrt{2}\alpha e^{-i\omega_z t}z/z_0+(z/z_0)^2)=-\frac{1}{2}(-\alpha^2e^{-2i\omega_zt}+(z/z_0-\sqrt{2}\alpha e^{-i\omega_z t})^2)$$ If we write the coherence amplitude as $\alpha=|\alpha|e^{i\delta}$, the first term in the bracket can be expressed with: $$-\alpha^2e^{-2i\omega_zt} =-|\alpha|^2e^{-2i(\omega_zt-\delta)}=-|\alpha|^2\cos (2\omega_zt-2\delta)+|\alpha|^2i\sin (2\omega_zt-2\delta)$$ Notice that: $$-|\alpha|^2\cos (2(\omega_zt-\delta))=-|\alpha|^2+2|\alpha|^2\sin^2 (\omega_zt-\delta)$$ the second term on the other hand can be written as: $$(z/z_0-\sqrt{2}|\alpha|(\cos (\omega_zt-\delta)-i\sin (\omega_zt-\delta)))^2$$ $$=z^2/z_0^2-2\sqrt{2}|\alpha|z/z_0(\cos (\omega_zt-\delta)-i\sin (\omega_zt-\delta))$$ $$+2|\alpha|^2(\cos^2 (\omega_zt-\delta)-2i\cos (\omega_zt-\delta)\sin (\omega_zt-\delta)-\sin^2 (\omega_zt-\delta))$$ $$=(z/z_0-\sqrt{2}|\alpha|\cos (\omega_zt-\delta))^2+2\sqrt{2}|\alpha|z/z_0i\sin (\omega_zt-\delta)$$ $$-4|\alpha|^2i\sin (\omega_zt-\delta)\cos (\omega_zt-\delta)-2|\alpha|^2\sin^2(\omega_zt-\delta)$$ With: $$-2|\alpha|^2i(2\sin (\omega_zt-\delta)\cos (\omega_zt-\delta))=-2|\alpha|^2i\sin (2(\omega_zt-\delta))$$ we get the following expression for our exponent term: $$-\frac{1}{2}\bigg((z/z_0-\sqrt{2}|\alpha|\cos (\omega_zt-\delta))^2+2\sqrt{2}|\alpha|z/z_0i\sin (\omega_zt-\delta)-|\alpha|^2-|\alpha|^2i\sin (2(\omega_zt-\delta))\bigg)$$ So the time evolution of the initial coherent state is: $$\Psi_\alpha (z,t)=\frac{1}{\sqrt{\sqrt{\pi}z_0}} e^{-\frac{1}{2}(z/z_0-\sqrt{2}|\alpha|\cos (\omega_zt-\delta))^2}e^{-i\omega_z t/2}e^{-\sqrt{2}|\alpha|z/z_0i\sin (\omega_zt-\delta)}e^{\frac{|\alpha|^2}{2}i\sin (2(\omega_zt-\delta))}$$ The probability density is then simply given by: $$|\Psi_\alpha (z,t)|^2=\frac{1}{\sqrt{\pi}z_0} e^{-(z/z_0-\sqrt{2}|\alpha|\cos (\omega_zt-\delta))^2}$$ If we only consider real $\alpha$ we can set $\delta=0$ so we get $\cos (\omega_zt-\delta)=\cos (\omega_zt)$. This leads us to following initial state: $$\Psi_\alpha (z,0)=\frac{1}{\sqrt{\sqrt{\pi}z_0}} e^{-\frac{1}{2}(z/z_0-\sqrt{2}|\alpha|)^2}$$ The probability density now becomes: $$|\Psi_\alpha (z,t)|^2=\frac{1}{\sqrt{\pi}z_0} e^{-(z/z_0-\sqrt{2}|\alpha|\cos (\omega_zt))^2}$$

Figure 2: Shows the time evolution of the probability density for the initial coherent state $\psi_\alpha(z,0)$ and compares
its analytical solution $\psi_\alpha(z,t)$ to the numerical calculated result from the above described Crank Nicolson
method $\psi (z,t)$. Notice however that one has set $m=m_e$, $\omega_z=110\cdot 2\pi$ kHz and $\alpha=2.5$.

References
[1] https://en.wikipedia.org/wiki/Crank%E2%80%93Nicolson_method
[2] https://en.wikipedia.org/wiki/Quantum_harmonic_oscillator

To get the code go to my GitHub repository 1D-Crank-Nicolson-Method

View Code

"""
The code below was written by @author: https://github.com/DianaNtz and is an 
implementation of the 1D Crank Nicolson method. It solves in particular the 
Schrödinger equation for the quantum harmonic oscillator. For more details on 
the code requirements and licences see 
https://github.com/DianaNtz/1D-Crank-Nicolson-Method.
"""
import numpy as np
import matplotlib.pyplot as plt
import os
import imageio
filenames = []
#some initial values
hbar = 1.05e-34
mass = 9.11e-31 #mass electron
wz=110*2*np.pi*1000 #freuquency in Hz
z0=np.sqrt(hbar/(wz*mass))
nz=2**9
dt=1*10**(-8) #dt in s
tfinal=2*np.pi/wz 
time_steps=int(np.round(tfinal/dt))
t=0
zmax=6.6*z0  #zmax in m
zmin=-6.6*z0 #zmin in m
dz=(zmax-zmin)/(nz-1)
n=np.linspace(-nz/2,nz/2-1,nz)
z=n*dz
psi0=np.exp(-((z)/z0)**2/2)
norm0=np.sum(psi0*np.conjugate(psi0))*dz
psi0=psi0/np.sqrt(norm0)
psi1=np.exp(-((z)/z0)**2/2)*2*z/z0
norm1=np.sum(psi1*np.conjugate(psi1))*dz
psi1=psi1/np.sqrt(norm1)
absalpha=2.5
psico=np.exp(-((z-z0*np.sqrt(2)*absalpha)/z0)**2/2)
normco=np.sum(psico*np.conjugate(psico))*dz
psico=psico/np.sqrt(normco)
#psi=(1/(np.sqrt(2)))*(psi1+psi0)
psi=psico
Vz=0.5*wz**2*z**2*mass
a=(1j*dt/hbar)/((4.0*mass*dz**2)/(hbar**2))
b=np.empty(nz, dtype=complex)
c=np.empty(nz, dtype=complex)
for i in range(0,nz):
    b[i]=1.0+0.5*dt/hbar*1j*(hbar**2/((dz**2*mass))+Vz[i])
    c[i]=1.0-0.5*dt/hbar*1j*(hbar**2/((dz**2*mass))+Vz[i])
#setting up matrices A and B
A=np.empty([nz, nz], dtype=complex)
B=np.empty([nz, nz], dtype=complex)
for i in range(0,nz):
    for j in range(0,nz):
        if   (j==i):
            A[i][j]=b[i]
            B[i][j]=c[i]
        elif (j==i+1):
            A[i][j]=-a
            B[i][j]=a
        elif (j==i-1):
            A[i][j]=-a
            B[i][j]=a
        else:
            A[i][j]=0.0
            B[i][j]=0.0            
invA=np.linalg.inv(A)
#starting loop for time iteration
for i in range(0,time_steps+1):
    psis=(1/(np.sqrt(2)))*(psi0*np.exp(-1j*wz*t/2)+psi1*np.exp(-1j*3*wz*t/2))
    rohco=np.exp(-((z-z0*np.sqrt(2)*absalpha*np.cos(wz*t))/z0)**2)/(z0*np.sqrt(np.pi)) 
    ka=B.dot(psi)
    psi=invA.dot(ka)
    #creating gif animation with imageio
    if(i%10==0): 
          print(i)
          ax1 = plt.subplots(1, sharex=True, figsize=(10,5))          
          plt.plot(z*10**3,rohco/10**(3),
          color='black',linestyle='-',linewidth=3.0,label="$|\psi_{α} (z, t)|^2$")
          #plt.plot(z*10**3,np.real(psis*np.conjugate(psis))/10**(3),
          #color='black',linestyle='-',linewidth=3.0,label="$|\psi_{s} (z, t)|^2$")
          plt.plot(z*10**3,np.real(psi*np.conjugate(psi))/10**(3),
          color='deepskyblue',linestyle='-.',linewidth=3.0,label = "$|\psi (z, t)|^2$")
          plt.xlabel("Position in [mm]",fontsize=16) 
          plt.ylabel(r'Probability density [1/mm]',fontsize=16)
          plt.ylim([0,70])
          plt.xlim([zmin*10**3,zmax*10**3]) 
          plt.xticks(fontsize= 16)
          plt.xticks([-0.08,-0.04,0,0.04,0.08])
          plt.yticks(fontsize= 16) 
          plt.text(0.04, 56.5,
          "t=".__add__(str(round(t*10**(6),1))).__add__(" $\mu$s"),fontsize=19 )
          plt.legend(loc=2,fontsize=19,handlelength=3,frameon=False) 
          filename ='bla{0:.0f}.png'.format(i/10)
          filenames.append(filename)    
          plt.savefig(filename,dpi=120)
          plt.close()
    t=t+dt
with imageio.get_writer('co2.gif', mode='I') as writer:
    for filename in filenames:
        image = imageio.imread(filename)
        writer.append_data(image)       
for filename in set(filenames):
    os.remove(filename)